Многоцикловое и истирающее воздействия дрейфующего ледяного покрова на морские гидротехнические сооружения (Взаимодействие вертикальных опор со льдом), страница 7

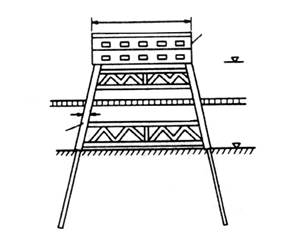
Рис.8. Конструкция опоры на шести колоннах D = 1,1 м в зал. Бохай (Сев.Китай)

Рассмотренные теоретические модели [ ], по существу, отличаются видом характеристики нагрузки-нелинейной функции F, зависящей от скорости движения ледового поля относительно опоры V_r. Обычно эту функцию, представленную в виде разложения в ряд, определяют экспериментально путем вычисления по данным опытов коэффициентов разложения a₀, a₁,a₃. В случае взаимодействия льда и сооружения эту функцию можно представить в виде

            при V_r³0                                (1.2.16)

                                         при V_r<0

Представление функции в виде (1.2.16) позволяет описать как релаксационные, так и гармонические автоколебания системы. Для моделей релаксационных колебаний в виде зубьев пилы) функцию F(V_r) упрощают и рассматривают F как ступенчатую. Анализ рассмотренных работ позволяет представить функции нагрузки в виде графиков (рис.10).

Как видно из рис.10, ни одна из рассмотренных выше моделей не учитывает роста нагрузки при увеличении V_r за счет вязкого сопротивления льда в зоне разрушения при прорезании опорой, а также за счет роста сил инерции при смешении обломков льда.

Большая часть существующих моделей описывает лишь релаксационные колебания, которые наблюдаются при небольших скоростях движения ледяного поля. Модель непрерывного дробления, помимо дискуссионности самого подхода к построению F(V_r) через R_c не отвечает условию спада нагрузки в момент разрушения в окрестности V_r=О.

Рис.10. Графическое представление функции нагрузки при расчете автоколебаний

льда и сооружений (F₀- значение предельной нагрузки при деформации

ледяного поля перед опорой d_кр)

1.2.3. Модели разрушения льда перед опорой.

Изучение контактной задачи воздействия движущейся ледяной плиты с опорой сооружения посвящено большое количество экспериментальных и теоретических исследовании, основной целью которых было раскрытие закономерностей формирования ледовой нагрузки. Значительно меньше работ ставили целью изучение процесса изменения силы во времени, т.е. рассматривали ледовую нагрузку, как случайный процесс. Как отмечалось выше, именно знание вероятностных характеристик ледовой нагрузки при решении контактной задачи позволяет оценить ее изменчивость в «малом» масштабе.

Основное внимание уделено экспериментальным исследованиям, так как в силу недостаточной изученности морского льда как материала и сложных граничных условий теоретические методы не позволяют в настоящее время получить приемлемое решение задачи.

Первые экспериментальные работы по исследованию контактной задачи для морского льда основывались на аналогии с определением твердости металлов. В основном рассматривались ударники сферической и конической формы [ ]. Результаты исследований использовались для определения прочности льда и позволили хорошо изучить и классифицировать физические процессы, происходящие при разрушении льда. Среднее контактное давление и прочность вычислялись на основе удельной энергии разрушения, которая была предложена в качестве энергетической прочностной характеристики льда. Но данный подход не давал распределения контактных давлений. С начала семидесятых за рубежом, в связи со строительством в Арктике первого сооружения (грунтового острова) в 1972г., начались интенсивные исследования льда как материала и взаимодействия ледяного покрова с сооружением. Вике и Ассур [  ] на основании проведенных лабораторных опытов установили, что прочность на сжатие обратно пропорциональна корню квадратному от площади разрушения. Мишель и Туссайнт [ ] предположили, что масштабный эффект относится только к малым контактным площадям, когда размер зерен сравним с площадью нагружения. Ряд мелкомасштабных экспериментов были проведены для изучения влияния масштабного эффекта на прочность льда [  ].