Многоцикловое и истирающее воздействия дрейфующего ледяного покрова на морские гидротехнические сооружения (Взаимодействие вертикальных опор со льдом), страница 6

где u_max, F₀ – соответственно максимальное перемещение и пиковое значение ледовой нагрузки в стадии установившихся колебаний; К - статическая жесткость конструкции.

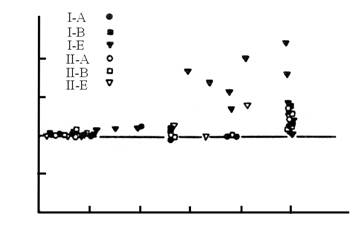
Анализ экспериментов показал, что диапазон  изменения разности максимальных значений перемещения моделей (тип I, II–Е)u_max минимального значения u_min описывается эмпирической зависимостью

,                                           (1.2.10)

Зависимость (1.2.10) подтверждается автономностью установившегося колебательного процесса, что говорит о наличии негативного демпфирования в колебательной системе и возникновении процесса ее автоколебаний. Математическая модель этого процесса описывается авторами в виде уравнения

,                                                    (1.2.11)

где М, С, К - соответственно масса, коэффициенты демпфирования и жесткости;

F(t) - ледовая нагрузка.

Рис.7. Зависимость динамического коэффициента D.M.F.

от скорости движения ледового поля V

Упруговяэкие деформации ледяного поля в расчет не принимаются. Предполагается, что нагрузка F(t) нарастает в пределах начальной фазы упругого деформирования конструкции до некоторого пикового значения F₀ при , затем резко падает до некоторой константы F_c, называемой силой разрушения льда при дроблении. Дальнейший процесс колебания в пределах цикла разрушения рассматривается при F(t)=F_c и начальных условиях

,                                                       (1.2.12)

Этой фазе соответствует время разрушения льда при дроблении T_c, которое заканчивается при повторном значении  и U=U_е. Затем вновь наступает фаза последующего упругого деформирования конструкции T_е, которая начинается при F=CU_e и заканчивается при F(t)=F₀. Таким образом возникает цикличность действия нагрузки. Если пренебречь силами демпфирования, то максимальные перемещения модели и период ее колебаний Т при действии льда могут быть описаны зависимостями

,                                        (1.2.13)

,                                            (1.214)

,                                                     (1.2.15)

где .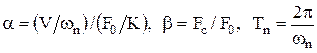

Сопоставление расчетных величин и результатов модельных опытов показало достаточно хорошее их совпадение при b=0,5. Предпринятая попытка построения функции нагрузки вплотную подходит к анализу взаимодействия с позиции теории автоколебаний (в данном случае релаксационных автоколебаний, так как предполагается статическое нагружение в каждом цикле до величины F_q).

Натурные наблюдения [ ] за вибрацией платформ выполнялись также в зал.Бохай (Северный Китай). Платформа состояла из эксплуатационного жилого и факельного блоков. Особенно интенсивно начали развиваться исследования после разрушения льдом в 1977 г. конструкций факельного и жилого блоков аналогичной платформы. На рис.8 приведена конструкция опоры из шести колонн D=1,1 м под жилой блок, на которой выполнялся комплекс наблюдений за ее состоянием и вибрацией под действием льда. Собственная частота колебания конструкции составляла 2 Гц. По данным измерений колебания опоры во времени с помощью дискретной трансформанты Фурье (преобразования Фурье) находилось силовое воздействие льда как функции времени.

Для аналитического описания динамического взаимодействия льда и опоры принималась модель Матлока [ ], которая позволила лишь описать импульсные воздействия льда продолжительностью 0,1 - 0,05 Т (Т - период воздействия) при длине зоны разрушения льда перед опорой Р=5-8 см. Значение коэффициента динамичности при импульсных воздействиях, найденное расчетным путем, было менее единицы.

Анализ экспериментов и расчетных данных показал, что модель Матлока описывает релаксационные колебания, предшествующие наиболее опасным (в смысле усталостной прочности) гармоническим колебаниям с максимальной амплитудой. Конструкции опор решетчато-колонного типа с малым размером колонн D=1,1 м оказались недостаточно устойчивыми к динамическому воздействию льда, поэтому рекомендуется в дальнейшем разработать конструкции с меньшим числом колонн, но увеличенного диаметра, для обеспечения жесткости конструкции.