Многоцикловое и истирающее воздействия дрейфующего ледяного покрова на морские гидротехнические сооружения (Взаимодействие вертикальных опор со льдом), страница 3

Для полного равновесия системы необходимо, чтобы все корни имели отрицательную действительную часть. Для свайных конструкций, как правило, достаточно учесть частоты ниже 15 Гц.

Исследование корней уравнений движения позволяет установить устойчивость в малом, т.е. при малых амплитудах. Однако с ростом амплитуда все более проявляется нелинейность системы: при достижении достаточных скоростей относительного движения прочность льда переходит в зону стабилизированного (постоянного) значения характеристики  и эффект негативного трения исчезает. В результате рост амплитуды замедляется и колебания стремятся к предельному циклу. Таким образом, характеристики предельного цикла могут быть получены путем интегрирования уравнения движения (6.3). Существование предельного цикла вытекает из соображений энергетического баланса системы. Энергия, отбираемая сооружением у ледяного поля не может расти неограниченно с ростом амплитуды, тогда как диссипация энергии за счет демпфирования монотонно возрастает. Рано или поздно система приходит в состояние, когда изменение полной энергии системы равно нулю за один цикл колебаний.

Режим колебаний сооружения может быть неустановившимся, установившимся с постоянной амплитудой и частотой и случайным (со случайной частотой и амплитудой). Последний является наиболее общим случаем, однако с точки зрения надежности сооружений наиболее опасным является установившийся режим из-за возможности резонансных колебаний (особенно на низких собственных частотах). Верхняя граница частоты колебаний под действием льда может быть определена по формуле

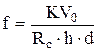                                                                        (1.2.4)

где К - изгибная жесткость конструкции на уровне действия льда, остальные обозначения прежние. Эта формула не учитывает деформацию льда и инерцию системы

В рамках общепринятой теории автоколебаний модель Маатенена не имеет достаточно четкой математической формулировки, не выделен нелинейный член в уравнении (1.2.3), который обеспечивает устойчивость системы и наличие предельного цикла. Характеристика внешнего трения (нагрузка как функция относительной скорости F(V)) принимается подобной изменению предельной прочности образца на одноосное сжатие в зависимости от скорости его загружения. Модель описывает идеализированный физический процесс, при котором в каждый момент времени имеет место непрерывное предельное состояние, предшествующее дроблению льда в зоне контакта, причем усилие при начальном дроблении определяется величиной V_r и заданной прочностью образца . В то же время в реальных условиях этот колебательный процесс протекает при условиях взаимодействия опоры с разрушенными и неразрушенными зонами льда, зависящими от геометрических, кинематических и физических параметров льда и габаритов сооружения.

При моделировании использовался лед с уретановыми добавками для снижения изгибной прочности и модуля деформации в соответствии с линейным масштабом моделирования 1:10. При моделировании ледяное поле надвигалось на модель сооружения, геометрическая жесткость которого варьировалась за счет изменения закрепления конструкции по высоте в различных опытах. Для измерения усилий и ускорения применялись датчик напряжений и акселерометры с соответствующей регистрирующей аппаратурой. Диаметр модели опоры во всех опытах был одинаковым – 103 мм. Скорость движения ледяного поля при моделировании плавно возрастала от 3 до 100 мм/с. Жесткость модели конструкции составляла 1,25 и 8,1 кН/мм.

На рис.2 (а, б, в) приведены примеры записей ледовой нагрузки в опытах на моделях опор с разной частотой собственных колебаний.

При малых скоростях движения ледяных полей все записи нагрузок имеют пилообразный вид (релаксационные колебания). С увеличением скорости возникают гармонические колебания моделей с частотой, близкой к нижней собственной частоте w₁ независимо от характера разрушения ледяного поля перед моделью.