Многоцикловое и истирающее воздействия дрейфующего ледяного покрова на морские гидротехнические сооружения (Взаимодействие вертикальных опор со льдом), страница 5

Колебание верхней части конструкции описывается с помощью уравнений колебаний жесткого тела

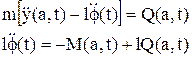,                                                           (1.2.8)

Обозначения даны на рис.4.

Для нижних частей конструкции применяются уравнения поперечных колебаний балок под действием нагрузок q(x) с учетом сил демпфирования. Для расчета фундаментной части конструкции используется гипотеза коэффициента постели. Место сопряжения верхней жесткой части конструкции с нижней балочной частью может иметь податливость при относительном повороте.

Решение задачи о колебании всей системы конструкции в целом, ввиду нелинейности ледовой нагрузки  может быть выполнено только численными методами. Для анализа общей устойчивости системы функция  может быть линеаризована путем разложения в ряд Маклорена. Устойчивость системы анализировалась с помощью построения Гамильтониана, H(t) как функционала Ляпунова. При H³0,  система устойчива. Первое условие Достигается всегда, а для выполнения второго условия  необходимо, чтобы энергия возмущающих сил не превышала энергию демпфирования системы.

Модель Тояма и др. [  ]. Дальнейшее развитие динамический метод расчета взаимодействия льда и сооружения с позиций автоколебаний получил в работе [ ]. Теоретическая модель строилась на основе данных лабораторных исследований.

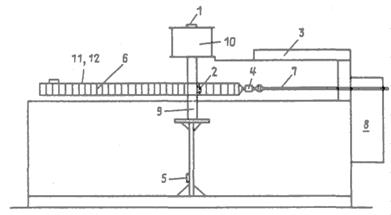
Рис. 6. Установка для проведения модельных опытов: 1 -верхний акселерометр; 2 - нижний акселерометр и датчик перемещений; 3 - элемент жесткости для закрепления массы модели; 4, - датчик давления; 5 - датчик напряжения; 6 - модельное ледовое поле; 7 - тяговый винт; 8 - привод и двигатель; 9 - испытываемая модель; 10 - основная масса модели; 11- направляющий рельс; 12 - тележка для закрепления и перемещения ледового поля.

На рис. 6 приведена схема расположения установки, оборудования и аппаратуры для проведения опытов.

Испытывались модели двух типов конструкций - моноподов (отдельно стоящие колонны, тип I ) и варианта двухколонной опорной части сооружения (тип II ) с расстоянием между центрами колонн 32 см. Диаметр колонн во всех случаях был равен 7,6 см.

В качестве модельного ледяного поля использовался слой льда толщиной 3-8 см столбчатой структуры, выпиливаемый из натурального ледяного поля, имеющего толщину 30 см. Прочность столбчатого льда на сжатие при испытании образцов поперек волокон (вдоль поверхности ледяного поля) изменялась от 0,7 до 1,4 МПа. Скорость перемещения модельного ледяного поля в опытах варьировалась от 0,2 до 4,8 см/с. Гидродинамический эффект взаимодействия модели-опоры и воды был мал и параметр демпфирования изменялся в пределах 0,0018-0,0023. Модели опор имели разную частоту собственных колебаний w_n которая имела следующие значения:

а) первый тип модели (монопод): I – F, I – А, I – В, I- E соответственно , 16.00; 4.02; 1.27 Гц.

б) второй тип модели: II–F, II–A, II–B, II–Е соответственно ; 14.7; 4.01; 1.21 Гц.

Во всех случаях, за исключением начального этапа загружения, в опытах наблюдались периодические воздействия ледовой нагрузки и соответственно колебания моделей. В то же время результаты экспериментов существенной зависели от частоты собственных колебаний моделей и скорости движения ледяного поля V . При испытаниях моделей, имеющих большую жестокость (F, A, B), при малых скоростях перемещения ледяного поля (V=0,2 – 0,6 см/с) диаграммы загружения и перемещения моделей имеют пилообразный характер с периодом порядка нескольких секунд. Для гибких конструкций моделей (Е) характерно установившееся гармоническое колебание величины нагрузок и деформаций при больших скоростях движения ледяного поля.

По результатам экспериментов вычислялся коэффициент динамики, значения которого приведены на рис. 7.

Коэффициент динамики D.M.F. определялся по формуле

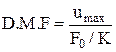,                                                                  (1.2.9)