Многоцикловое и истирающее воздействия дрейфующего ледяного покрова на морские гидротехнические сооружения (Взаимодействие вертикальных опор со льдом), страница 2

Для аналитического описания процесса взаимодействия используются несколько моделей автоколебаний льда и сооружения, основанных на разных расчетных предпосылках и допущениях.

Модель Матлока [  ]. Близкие к релаксационным колебания опоры могут быть достаточно хорошо описаны с помощью известной модели Матлока [  ]. Механический аналог этой модели приведен на рис.6.1. Ледовое поле представляется в виде “гребенки” с упругими зубьями, которая движется со скоростью V, причем зубья вступают в контакт с сооружением и при критических деформациях d_кр разрушаются. Значение d_кр может зависеть от скорости деформации [  ] и изменяться от цикла к циклу. Эта модель соответствует идеальной безынерционной модели упругохрупкого разрушения льда с нулевым значением сил сопротивления льда при значении скорости его смещения относительно опоры, отличной от нуля.

Возможны модификации модели Матлока, например, вместо d_кр может быть принято предельное значение нагрузки (прочности зубьев “гребенки”), а под Р можно понимать размер зоны разрушения льда перед опорой [ ]. Модель Матлока имеет простой механический смысл и нашла достаточно широкое применение в исследованиях при интерпретации результатов опытов [   ].

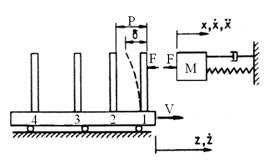
Рис.1. Механический аналог взаимодействия льда и сооружения (схема Матлока [  ])

Модель Маатененна [  ]. Наибольшее развитие динамический метод взаимодействия льда и сооружения с позиций автоколебаний получил в работах Маатененна [  ]. В основу теоретических рассуждении Маатенена положен экспериментальный факт наличия у кривой R_c(f) или  двух ветвей-нарастания прочности при малых значениях и уменьшения прочности с ростом при больших скоростях загружения. В связи с этим при увеличена скорости движения опоры относительно льда внешнее воздействие может убывать (как функция скорости нагружения), что и является причиной возникновения автоколебаний. В рамках теории автоколебаний этот эффект трактуется как увеличение негативного трения в системе.

Для оценки прочности льда от скорости относительного движения V_r принята зависимость

,                                                               (1.2.2)

где D - диаметр опоры;

- эмпирическая зависимость прочности на одноосное сжатие от ;

q- полярный угол;

V_r - скорость движения опоры относительно ледяного поля, определяемая зависимостью;

, при этом

- скорость движения ледяного поля;

- движения кромки льда и опоры в точке контакта n.

По значению  оценивается значение нагрузки F. При решений  практических задач для гибких опор значением пренебрегают. Уравнение автоколебаний опоры при взаимодействии со льдом представляется в виде [ 277 ]

,                                        (1.2.3)

где  - матрицы жесткости, демпфирования (позитивного трения) и масс;

- постоянная нагрузка при скорости движения льда V₀;

[j] - матрица негативного трения, которая изменяется с ростом амплитуды и скорости нагружения в соответствии с (2).

Амплитуду колебаний определяет соотношение позитивного и негативного демпфирования ([d]-[j]) в системе. Позитивное демпфирование системы включает в себя внутреннее трение самой конструкции и основания, гидро- и аэродинамическое сопротивление, трение льда и сооружение, а также диссипацию энергии при разрушении льда на обломки.

Гидродинамическое сопротивление и внутреннее трение в системе изменяется от 2 до 10%. Следует принимать для сооружений в воде без учета льда эти величины равными 3-6% для низких частот собственных колебаний. Колебания возникают в случае динамической неустойчивости системы (3). Условия устойчивости определяются комплексно-сопряженными парами корней линеаризованных уравнений движения, например для j-формы

, где - демпфирование; w_j - угловая скорость.

Если р_j<0, колебания затухают по экспоненте, и нагрузка F во времени постоянна. Если р_j>0, колебания нарастают экспоненциально и возникают автоколебания, причем для этого достаточно минимального отклонения системыот положительного равновесия (например, за счет флюктаций прочности во льду).