Строительство и архитектура \ Строительная механика

Многоцикловое и истирающее воздействия дрейфующего ледяного покрова на морские гидротехнические сооружения (Взаимодействие вертикальных опор со льдом), страница 4

Рис.2. Процесс изменения ледовой нагрузки при автоколебаниях модели опоры

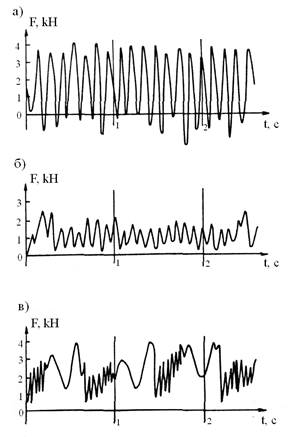
при разной частоте собственных колебаний

В случае более гибких моделей резонансные колебания возникают при скоростях движения ледяного поля, начиная с V =30 мм/с и продолжаются до максимально возможных в опыте скоростей V 100 мм/с, причем динамические нагрузки имеют наибольшие значения в широком диапазоне изменений скорости до 70 мм/с. При увеличении жесткости резонансные колебания возникают при тех же минимальных значениях скорости движения ледяного поля, однако исчезают при скоростях движения более 90 мм/с.

Анализ результатов опытов показывает, что при малых скоростях движения ледяного поля частота внешнего воздействия (ледовой нагрузки) зависит от динамических свойств сооружения и размеров зоны разрушения ледяного поля перед опорой, с увеличением скорости влияние последнего фактора уменьшается и возникают гармонические автоколебания системы. С ростом гибкости и массы системы увеличивается опасность возникновения автоколебаний, если не предусмотрены специальные виброзащитные элементы.

Модель Ранта-Рети [ ]. Эта модель представляет собой усовершенствованную модель автоколебаний при взаимодействии льда и гибких опор с непрерывным разрушением льда дроблением Маатенена [  ].

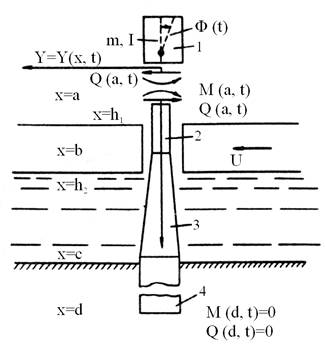
Решение задачи получено для случая взаимодействия льда с симметричной в плане конструкцией опоры (рис. 4), состоящей из четырех частей: верхней части 1 - жесткого тела, переходной части 2 в виде тонкой балки постоянного сечения, средней части 3 - балки с линейным уширением книзу и части 4, заглубленной в грунтовое основание.

Возможны три типа распределения ледовой нагрузки на конструкцию опоры на участке h1<x<h2 от действия дрейфующего со скоростью V ледового поля:

а) q(t, x)=0 - при отсутствии контакта льда и сооружения;

б) q(t, x)=qk при - кинетическая стадия нагружения, где - скорость деформации конструкции;

в)  - кинематическая стадия нагружения при разрушении льда за счет дробления.

При кинематической стадии загружения нагрузка представляется в виде линейной возрастающей во времени функции. Все стадии загружения чередуются последовательно одна за другой, вызывая колебания конструкции маяка. Если цикл изменения нагрузки включает только кинематическую и кинетическую стадии нагружения, то соотношение продолжительности этих фаз равно 3:1.

Учет влияния скоростей нагружения и дрейфа ледяных полей осуществляется путем введения в расчет линейно-кусочной аппроксимации зависимости

Рис. 6.4. Расчетная схема конструкции опоры

,                                                            (1.2.5)

а также уравнения типа (1.2.2)

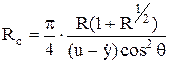,                                                     (1.2.6)

где - радиус опоры и его производная по высоте вместе приложения ледовой нагрузки (предполагается, что -мала);

u - скорость движения ледяного поля относительно неподвижной опоры.

На рис. 5 приведен график изменения зависимостей (1.2.6), (1.2.5), точка их пересечения соответствует совместному решению уравнений (1.2.6) и (1.2.5).

Ледовая нагрузка в кинематической стадии нагружения представляется в виде

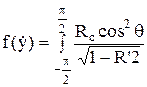,                                                                      (1.2.7)

sc
 
 
 

3
 

2
 

1
 

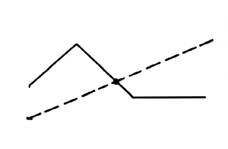
Рис. 5. Линейно-кусочная аппроксимация уравнений (1.2.5) и (1.2.6)

где - из решения уравнений (1.2.5), (1.2.6), зависящих от скоростей нагружения и дрейфа ледяных полей. Уравнения колебания конструкции опоры зависят от массы и жесткости его различных частей (рис. 4).

Скачать файл