Векторы и координаты, задачи на отношения

Векторы и координаты, задачи на отношения

Задача 1.26. Пусть A₁, B₁, C₁, – середины сторон BС, AC и AB треугольника ABC. Докажите, что для любых точек O и O₁ справедливо равенство

Задача 1.33. Пусть OABC – произвольный тетраэдр, AM – медиана грани ABC. Разложить вектор  по векторам , , .

Задача 1.34. В тетраэдре OABC точки M и N – середины ребер OB и OC. Разложить векторы , ,  по векторам , , .

1.30. Найти угол между векторами (–3; 4; 0) и (5; 0; –12). Система координат прямоугольная.

1.32. Векторы и  неколлинеарны. Найдите, при каком значении x векторы  и  будут коллинеарны.

1.43. Докажите, что четырехугольник с вершинами в точках A (7; 2; 4), B (4; –4; 2), C (6; –7; 8) и D (9; –1; 10) является квадратом.

2) Векторы  и  неколлинеарны. Найти значения x и y, при которых векторы  и  равны.

3) Используя скалярное произведение векторов, найти углы треугольника с вершинами A(–2; –3), B(2; 1), C(1; 4).

4) Точки M и N выбраны соответственно на основании BC и боковой стороне CD трапеции ABCD Прямые AM и BN пересекаются в точке K так, что AK=3KM, KN=2BK. Найти отношения CN:ND.

4) В тетраэдре ABCD точки M и N являются соответственно точками пересечения медиан граней ABD и BCD. Докажите, что вектор  коллинеарен вектору  и найдите отношение .

Задача 1.25. Дан правильный шестиугольник ABCDEF. Разложить векторы  и  по векторам  и  (рис. ).

Решение. Пусть точка O – центр правильного шестиугольника. Тогда ABCO и ABOF– параллелограммы (докажите это). Отсюда следует  и .

Задача 1.26. Пусть A₁, B₁, C₁, – середины сторон BС, AC и AB треугольника ABC. Докажите, что для любых точек O и O₁ справедливо равенство

                                                 

Решение. Покажем сначала, что если точка C₁ – середина стороны AB треугольника OAB, то . Проведем через точки A и B прямые параллельные OB и OA соответственно. Пусть E – точка пересечения этих прямых, тогда OAEB – параллелограмм, E – точка пересечения его диагоналей. По правилу параллелограмм сложения векторов: , отсюда

                                                        .                                               (1.5)

Аналогично запишем:

                                                                                                                       (1.6)

                                                                                                                       (1.7)

Складывая равенства (1.5)–(1.7), получаем требуемое.

Задача 1.27. Пусть M – точка пересечения медиан треугольника ABC. Доказать что

а)           

b)           

c)             . Здесь О – любая точка пространства.

Решение. Докажем равенство a). Пусть A₁ – середина сторон BС. Используя результат предыдущей задачи, имеем . По свойству точки пересечения медиан

                                                        .

Докажем теперь равенство b). Пусть A₁ – середина сторон BС. Используя тот же самый прием для треугольника MBC имеем . По свойству точки пересечения медиан . Отсюда следует равенство b).

Докажем равенство c). Запишем очевидные равенства:

, , .

Сложив все три равенства и учитывая b), получаем:

.

Задача 1.28. Даны вектора  и . Разложить вектор  по векторам  и .

Решение. Пусть . Раскрыв скобки и приведя подобные, получим . Поскольку разложение по неколлинеарным векторам единственно, то  и . Отсюда находим , .

Задача 1.29. Даны три вектора ,  и , каждые два из которых неколлинеарны. Найти их сумму, если вектор  коллинеарен вектору , а вектор  коллинеарен вектору .

Решение. По условию , . Из этих равенств получаем . Так как  и  неколлинеарны, то , . Отсюда следует  и , т. е.  и . Слодовательно, .

Задача 1.30. Дан треугольник ABC. На стороне BC взята точка M так, что BM:MC=2:1. Разложить вектор  по векторам  и.

Решение. Вектор .

Задача 1.31. Дан треугольник ABC. В каком отношении точка K делит сторону BC, если ?

Решение. Пусть . Отсюда . Как видим, . Это значит, что длина отрезка BK составляет  длины стороны BC, а длина отрезка CK – соответственно  длины стороны BC, т. е. точка K делит сторону BC в отношении .

Задача 1.32. Даны неколлинеарные векторы и . Найдите множество точек M таких, что .

Решение. Рассмотрим вектор  . Как видим, он коллинеарен вектору . Это означает, что точка M лежит на прямой AB. В частности, при точка M лежит на отрезке AB (почему?).

Задача 1.33. Пусть OABC – произвольный тетраэдр., AM – медиана грани ABC. Разложить вектор  по векторам , , .

Решение. Запишем очевидное равенство . Т. к. OM – медиана треугольника OBC, то . Отсюда .

Задача 1.34. В тетраэдре OABC точки M и N – середины ребер OB и OC. Разложить векторы , ,  по векторам , , .

Решение. Запишем очевидное равенство . Поскольку OM – медиана треугольника OBC, то . Отсюда .

Задача 1.35. (РЭА, 1996) Найти значение координаты x, при котором вектор  разлагается по векторам  и .

Решение. Пусть , тогда координаты векторов  связаны между собой тем же самым соотношением, т. е. одно векторное равенство равносильно трем скалярным:

                                                                

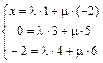
Из последних двух уравнений системы находим , , затем из первого уравнения находим .

Скалярное произведение.

Докажем основное свойство скалярного произведения:

                                                            .                                                    (1.8)