Векторы и координаты, задачи на отношения, страница 3

Задача 1.40. Вектор  коллинеарен вектору  и образует с осью Oz острый угол. Зная, что , найти координаты вектора .

Решение. По условию . Вычислим. Отсюда , т. е. . По условию угол между вектором  и вектором  должен быть острым, т. е. . Этому требованию удовлетворяет только , поэтому .

Задача 1.41. Векторы  и  — единичные и взаимно перпендикулярные. Найдите угол между суммой и разностью векторов  и , где , .

Решение. Имеем , . Учитывая, что модуль векторов  и  равен 1 и , вычисляем , , . Отсюда , т. е. угол между векторами равен .

Задача 1.42. Даны два неколлинеарных вектора , . Найдите вектор:

a)  направленный по биссектрисе угла между ними;

b)  перпендикулярный вектору .

Решение. Разложим искомый вектор  по векторам  и , т. е. представим ег в виде . Условие a) означает, что косинусы углов между ,  и между ,  одинаковы, т. е. должно выполняться равенство

                                                      .

Отсюда . Собирая в одной части члены, содержащие l, а в другой члены, содержащие m, получаем

.

Поскольку  (почему?), то , где k – некоторое число не равное нулю. Таким образом, ,  и .

Условие b) означает, что , или , где k – некоторое число не равное нулю. Отсюда искомый вектор

                                                   .

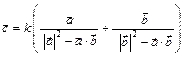Задача 1.43. Доказать тождество

                              

Решение. Запишем векторные равенства:

, ,

Возведем все три равенства в квадрат и сложим. Получим

            , откуда следует доказываемое тождество.

Задача 1.44^*. Дан треугольник ABC. Найдите геометрическое место таких точек M, что

                                                 

Решение. Сменим знак в обеих частях равенства и запишем его в виде

                                                  

Подставляя в него равенства , , , получаем . Раскрывая скобки, убеждаемся, что это тождество, т. е. искомое геометрическое место точек M – все точки пространства.

Задача 1.45. Пусть ABC – равносторонний треугольник со стороной 1. Найдите множество точек M таких, что

Решение 1. Введем прямоугольную систему координат Oxy так, что начало координат точка O – середина отрезка AB, ось абсцисс направлена по прямой AB (рис. ). Тогда вектор , точка C имеет координаты . Пусть точка M имеет координаты , тогда вектор . По условию . Таким образом, точка M лежит на прямой, перпендикулярной к AB на расстоянии  от точки B.

Решение 2. Отложим из вершины C единичный вектор , равный вектору . Пусть угол между векторами  и  равен j и  (рис. ). По условию . Величина  — это проекция отрезка CM на прямую CD. Таким образом, проекция точки M на прямую CD совпадает с точкой D, т. е. точка M лежит на прямой, перпендикулярной к AB на расстоянии 1 от точки C..

Задача 1.46.^* (НГУ) Какой наименьший угол могут образовать векторы  и ?

Решение. Если угол j между векторами  и наименьший, то косинус угла будет наибольшим. Вычислим косинус этого угла по формуле (1.12). Имеем

                                          ,

                                  ,

                                       .

Отсюда .

Значение  будет максимальным когда квадратный трехчлен в знаменателе будет наименьшим. Выделяя полный квадрат, находим . Отсюда наибольшее значение , оно достигается при . Наименьший угол между векторами равен .

Задача 1.47.* Пусть H — точка пересечения высот, точка O — центр окружности, описанной около треугольника ABC. Доказать, что .

Решение. По условию задачи вектор  перпендикулярен вектору , т. е.

                                                         .                                              (1.13)

Кроме того, , т. е.