Методы анализа кредитоспособности в долгосрочном периоде, страница 2

Для наглядности распишем i-тую строку равенства (6.1):

W_i /W₁ х W₁ + ... W_i /W_n х W_n = W_i + ...+ W_i = n x W_i.

Заметим, что это условие выполняется для любой строки выражения (6.1).

Пусть дана квадратная матрица А = (a_ij) nхn. Если существует ненулевой вектор Х и вещественное значение g, такие, что выполняется равенство А х X = g х X, тогда g — собственное значение матрицы А, а Х— собственный вектор.

В теории линейной алгебры доказана теорема: g является собственным значением матрицы А тогда и только тогда, когда g — корень характеристического уровня:

, где Е - единичная матрица,

т.е. .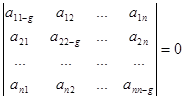

Для выщеуказанного уравнения существует n корней, в основном — комплексных.

Из уравнения 6.1 и вышеуказанного следует, что n — собственное значение матрицы A, W — соответствующий собственный вектор, тогда можно доказать, что n — единственное значение для данного собственного вектора.

Пусть теперь для определенности n — максимальное собственное значение, тогда из 6.1 следует:

A x W = g_max x W, где g_max — максимальное собственное значение.

Таким образом, функция принадлежности строится так: строится матрица А, для нее отыскивается g_max, затем выписывается система линейных уравнений: А х W = g_max х W, затем W_i нормируются, т. е. делятся на их сумму. При этом, если

тогда результаты вычислений приемлемы.

ПРИМЕНЕНИЕ ЭТОГО МЕТОДА ДЛЯ ФОРМИРОВАНИЯ АГРЕГИРОВАННЫХ ПОКАЗАТЕЛЕЙ КРЕДИТОСПОСОБНОСТИ

Для применения этого метода на практике в качестве матрицы А используется матрица парных сравнений (полученных экспертным путем) весомости для показателей, формирующих агрегированный показатель кредитоспособности, который сравнивается с нормативным агрегированным показателем кредитоспособности для данного предприятия (среднеотраслевым показателем). Нормативный агрегированный показатель кредитоспособности формируется на базе соответствующих составляющих его отдельных нормативных показателей финансовой устойчивости и других показателей, которые влияют на кредитоспособность предприятия, т. е. формализованных показателей управляемости системы на предприятии, рисковости данного вида деятельности, степени профессиональности менеджерского персонала на данном предприятии, показателя технологичности производственной системы.

Матрица парных сравнений составляется по следующим принципам:

—  при сравнении весомости показателей исходят из 10-балльной системы;

—  оценки, полученные с одной стороны от главной диагонали матрицы, должны быть обратны оценкам, находящимся с другой стороны от главной диагонали;

—  сами оценки составляются исходя из следующих принципов (табл. 6.7).

Таблица 6.7

Оценки значимости показателей

Если значимость показателя меньше значимости сравниваемого с ним, то ставится оценка 1/W.

На основе экспертных оценок строится матрица парных сравнений, для которой определяется максимальное собственное значение, затем после выписывания системы линейных уравнений определяется собственный вектор и нормируются его компоненты. После этого компоненты показывают веса разных показателей в долях от единицы. Поэтому агрегированный показатель определяется как сумма произведений значений составляющих его показателей на соответствующие весовые коэффициенты, определенные вышеуказанным путем.