Электродинамика газового разряда. Типы разрядов в постоянном электрическом поле. Статическое состояние в окрестности эмитирующего катода (модель Маккоуна). Искровой и коронный разряды, страница 8

1). Амбиполярная диффузия. В слабоионизировавнной плазмедавление плазменной компоненты много меньше давления нейтральной компонентыи электрон- ионные столкновения играют существенной роли по сравнению со столкновениями заряженных частиц с молекулами нейтрального газа. В этом случае нейтральная компонента представляет собой неподвижную среду, в которой диффундируют электроны и ионы. Задача о медленном изменении состояния плазмы сводится к задаче диффузии. Попадая на стенки, электроны и ионы оседают на них и затем нейтрализуются. Стенки являются «поглотителями » зарядов, плотность плазмы у стенок почти равна нулю. В окрестности стенок возникают радиальные (поперечные) градиенты концентрации и поперечные потоки от середины объема к стенкам. Это не должно приводить к возникновению тока, так как иначе в плазме возникло бы сильное разделение зарядов. Следовательно, потоки электронов и ионов должны быть одинаковыми. Это приводит к амбиполяроной диффузии при которой ионы и электроны переносятся с одинаковой скоростью. Таким образом, диффузия происходит без тока

.

Особенностью диффузии заряженных частиц в случае слабой ионизации и большой концентрации нейтральных частиц, является малая длина свободного пробега заряженных частиц. Медленность процессов и большая частота соударений с нейтральными частицами позволяет пренебречь инерциальными членами в уравнениях движения;

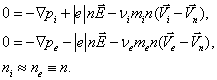
При амбиполярной диффузии в поперечном к столбу направлении, должны быть одинаковы поперечные скорости ионов и электронов. Это позволяет получить представление для поперечного электрического поля

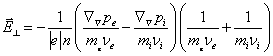.               (15.10)

Уравнения движения заряженных частиц можно представить в виде

,  - плотности потоков электронов и положительных ионов. Потоки представляются  в виде сумм диффузионных и дрейфовых составляющих:

,             ,          

-коэффициент диффузии,  - постоянная Больцмана,  - подвижность.

Между коэффициентами диффузии и коэффициентами подвижности имеет место соотношение Эйнштейна

.

Поле (15.10) можно представить в виде

и, следовательно имеет место представление

,                                   (15.10.А)

где  - коэффициент амбиполярной диффузии. Обычно  и имеет место представление

.

Формула (15.10.А) представляет собой закон Фика для диффузии, но с новым коэффициентом - с коэффициентом диффузии . Физически коэффициент  выступает как результат возникновения в плазме поперечного поля , которое удерживает электроны и не дает им «убегать» от ионов. Одновременно, это поле «подталкивает» ионы, обеспечивая режим амбиполярной диффузии.

Уравнение, описывающее распределение концентрации заряженных частиц с учетом ионизации в статическом состоянии можно представить в виде

.                                       (15.11)

Рассмотрим модель амбиполярной диффузии Энгеля и Штеенбека. Для этого уравнение (15.11) решим в цилиндрической геометрии с граничными условиями

.

Условие  называется условием Шоттки. Имеет место представление

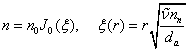, где  - функция Бесселя, . Так как , то 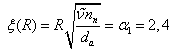 - первый корень бесселевой функции. Таким образом, имеет место связь между параметрами

.

Температура ионной компоненты близка к температуре окружающей среды. Последнее соотношение может быть использовано для нахождения температуры электронной компоненты.

2). Рекомбинация. Если относительная скорость столкновения электрона с ионом мала, то они с большой вероятностью могут рекомбинировать и образовывать нейтральный атом. Уменьшение концентрации плазменной компоненты из за рекомбинации можно описать введя отрицательный источник в уравнение непрерывности. Этот член будет пропорционален . Пренебрегая эффектом диффузии, уравнение неразрывности заряженной компоненты запишем в виде нелинейного уравнения

, или

.

Интегрирование дает следующий результат

.

После того как концентрация станет существенно меньше своего начального значения, она будет убывать  по закону

.

При низких значениях концентрации главную роль начинает играть диффузия. Временная зависимость в этом режиме радикально изменяется: концентрация плазменной компоненты уменьшается со временем экспоненциально.