Электродинамика газового разряда. Типы разрядов в постоянном электрическом поле. Статическое состояние в окрестности эмитирующего катода (модель Маккоуна). Искровой и коронный разряды, страница 6

Если  - длина свободного пробега электрона в газе, то вероятность того, что электрон пройдет без столкновений расстояние в промежутке () описывается экспоненциальным законом . При использовании нормировки

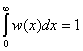
будем иметь представление

.                         (15.5)

Если электрон пройдет вдоль поля расстояние , то он приобретет энергию . В том случае, если  ( - энергия ионизации), то в принципе электрон может ионизировать молекулу газа. Расстояние , проходимое электроном без столкновения должно быть не меньше, чем  и формула (15.5) принимает вид

.

.                 (15.6)

На пути  электрон по определению порождает  пар зарядов. Длина свободного пробега  обратно пропорциональна давлению  и формуле (15.5) можно придать вид эмпирической закономерности Таунсенда

,                        (15.7)

где  - эмпирические, характерные для каждого газа константы. Отметим, что формула (15.7) не применима для случая сильных полей, когда

Если положения катода и анода даются значениями , то электронный ток на аноде имеет вид

.

Каждый электрон, вышедший из катода и дошедший до анода приводит к наличию  электронов в этом промежутке. Новых электронов на единицу меньше: . Поэтому возникает  положительных ионов, двигающихся к катоду. По пути эти ионы производят ионизацию газа. Придя на катод, они выбивают из него электроны. Возникает вторичная эмиссия. Число этих вторичных электронов обозначим .

Выясним влияние этих , выбитых электронов на лавинный процесс. Каждый электрон на промежутке катод – анод создает  пар заряженных частиц. Количество  ионов создаст  штук электронов, выбитых из катода. Если это число больше единицы, то начальные электроны будут «воспроизводиться». создадут  электронов и так далее. Из одного начального электрона, вышедшего из катода, получится на аноде

электронов. Ели , то этот ряд сходится:

и возникнет анодный ток

, где  - начальный ток из катода.

Если  бесконечно малый первичный ток, то условием возникновения самостоятельного разряда будет требование обращения знаменателя в ноль

.                                   (15.8)

Параметр  является своеобразным «коэффициентом усиления» для возникновения пробоя, он составляет величину порядка .

С учетом (15.7) из условия (15.8) получим выражение для коэффициента ионизации

.            (15.9)

Потенциал зажигания. Электрическое поле  в формуле (15.9) называется критическим или полем зажигания. Так как , то соответствующий критический потенциал зажигания имеет вид

.

Любопытно, что потенциал зажигания имеет минимум при значении параметра . Обращение тока в бесконечность является следствием грубой идеализации: отсутствие учета влияния диссипации.

Аналогично рассматривается ионизация под действием ионов. Подвижность тяжелых ионов гораздо меньше, чем у электронов. Поэтому в начальной стадии имеет место нестационарный (переходной) процесс. В самом начале процесса в разрядном промежутке накапливается положительный заряд. Постепенно накопление ионов прекращается, поток ионов на катод достигает величины, равной потоку электронов на анод.

Устанавливается самостоятельный стационарный разряд. В таком разряде имеется однозначная связь разности потенциалов в газовом промежутке и силой тока (вольт – амперная характеристика разряда). Типичная вольт – амперная характеристика изображена на Рис.15.1. На характеристике ток не зависит от времени (например, в точке G). Вольт – амперная характеристика разбивает плоскость () на две части I и II, которым соответствуют неравновесные режимы. В области I происходит нарастание разрядного тока, а в области II – уменьшение тока. На вольт – амперной характеристике имеет место стационарность: .

Реальный процесс пробоя газоразрядного промежутка – явление исключительно сложное и многообразное. В нашем рассмотрении использовалась идеализация: в однородном поле ионизация происходит однородно. На самом деле это справедливо только при не слишком больших значениях параметра .