Электродинамика газового разряда. Типы разрядов в постоянном электрическом поле. Статическое состояние в окрестности эмитирующего катода (модель Маккоуна). Искровой и коронный разряды, страница 4

                                           ,                                (15.4)

где - упорядоченная скорость электронов:

                               ,

 - подвижность электрона.

Из формул (15.3) и (15.4) получаем представление

                               .                    (15.4.A)

Создается иллюзия, будто температура электронов пропорциональна квадрату электрического поля. На самом деле это не так.

Введем понятие длины свободного пробега электронов

С учетом формулы (15.4.А) получаем

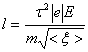
и сама формула (15.4.А) приводится к виду

                                           .

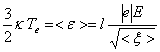Для величины длины свободного пробега есть еще одно представление: , (-концентрация электронов, – сечение рассеяния электрона молекулой). Для не слишком слабых полей, когда , длина свободного пробега не зависит от энергии электрона. В такой ситуации температура  пропорциональна напряженности электрического поля . Подвижность при этом представляется в виде

                                           .

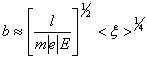15.6. Частота упругих соударений электронов с нейтральными и заряженными частицами.

1). При упругих соударениях электронов с нейтральными частицами заряд электронов не играет роли. Так как время взаимодействия частиц гораздо меньше времени свободного пробега, то влияние внешних полей проявляется слабо. Пусть  - площадь сечения (поперечник рассеяния) одной из нейтральных частиц. Поперечник рассеяния электрона гораздо меньше, чем поперечник рассеяния нейтральной частицы. По этому будем пользоваться идеализацией бесконечно малого размера электрона (точечное приближение). Длина свободного пробега электронов представляется в виде

, где  - концентрация нейтральных частиц,  - радиус поперечника рассеяния. Возможно альтернативное определение длины свободного пробега

, где  - время свободного пробега электрона,  частота упругих соударений электронов с нейтральными частицами, . Получаем представление

.

Если концентрацию брать , то будем иметь

.

Более точное кинетическое описание дает значение коэффициента  приблизительно в два раза больше. Элементарные, наглядные рассуждения позволяют простым и коротким путем найти результат с точностью до численного коэффициента порядка единицы. При этом «схвачена» главная суть явления.

2). Характерные чертыдвижения электронов и ионов в плазме при отсутствии внешних полей определяется законами взаимодействия заряженных частиц. Происходит рассеяние частиц в электрическом поле, близком к кулоновскому. Различаются три типа элементарных актов: рассеяние электронов на ионах, электронов на электронах и ионов на ионах.

Оценим теперь частоту соударений электронов с ионами на основе довольно грубых представлений. Пусть через плазму проходит некоторый «пробный» электрон. Этот электрон испытывает акты рассеяния на своем пути. Центры рассеяния тяжелых частиц (ионов) можно считать неподвижными. Дифференциальное эффективное сечение рассеяния  определяется классической формулой Резерфорда

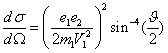, где индексы 1 и2 относятся к рассеивателю и рассеянной частицы,  - угол рассеяния,  - элемент телесного угла. Каждый акт рассеяния приводит к приводит к повороту траектории электрона на угол , При этом происходит уменьшение скорости по первоначальному направлению движения от  до . Акты рассеяния в подавляющем большинстве случаев происходят на больших расстояниях с малым изменением направления траектории. Имеет место картина рлавно извивающейся траектории. Направление ее непрерывно изменяется под действием многочисленных слабых импульсов. Эта картина резко отличается от ломаной траектории при столкновениях нейтральных частиц. В полностью ионизированной плазме почти все время заряженные частицы движутся свободно. При этом справедливо выполнение условия: кинетическая энергия заряженных частиц почти всегда гораздо больше потенциальной энергии взаимодействия. В «момент соударения» эти энергии становятся величинами одного порядка. Это позволяет приближенно ввести понятие радиуса поперечника рассеяния заряженной частицы :