Электродинамика газового разряда. Типы разрядов в постоянном электрическом поле. Статическое состояние в окрестности эмитирующего катода (модель Маккоуна). Искровой и коронный разряды, страница 5

, где  - радиус экранирования Дебая. В результате получаем

,       .

Взаимодействие заряженных частиц в грубом рассмотрении будет делаться следующим образом: заменяется плавно изгибающиеся траектории электронов на условные ломаные линии и эффект многих слабых взаимодействий заменяется на один сильный удар. Следует отметить, что поперечник рассеяния заряженных частиц уменьшается с ростом температуры.

Для длины свободного пробега будем иметь представление

, где коэффициент 2 учитывает аддитивное влияние ионов и электронов при условии .

Учитывая альтернативное описание

,         , получим оценочное описание частоты соударений электронов с ионами

.

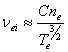Если концентрацию брать , то . Расхождение с кинетической теорией более значительно, чем в случае соударений с нейтральными частицами. Кинетическая теория дает:

.

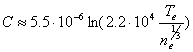Для полной характеристики кулоновского взаимодействия заряженных частиц в плазме нужно ввести параметры, характеризующие столкновения между идентичными частицами: электрон-электронные и ион-ионные столкновения. Расчет в этом случае осложняется необходимостью учитывать движение рассеивающих частиц. Это влияние отражается только на значении численного коэффициента в соответствующих формулах, а температурная зависимость имеет одинаковый характер. При  ион-ионные соударения происходят гораздо реже, чем электрон-электронные и электрон-ионные. С введением понятий длина свободного пробега и время свободного пробега вернемся к понятию плазма:

.

Это неравенство можно представить в ви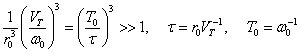де

, где  - среднее расстояние между частицами,  - период плазменных колебаний,  - время свободного побега. Таким образом, время свободного пробега в плазме должно быть меньше периода плазменных колебаний.

Польза от применения вышеприведенных не очень корректных приемов заключается в том, что имея такие пиближенные формулы, можно оперировть наглядными картинами при анализе основных физических процессов в плазме.

15.7. Самостоятельный разряд. Ионизация и пробой в постоянном поле. Потенциал зажигания. Необходимое (но не достаточное) условие ионизации атома или молекулы заключается в том, чтобы кинетическая энергия электрона превосходила энергию связи в атоме (молекуле). Эту энергию называют энергией ионизации. Но даже в такой ситуации, столкновение электрона с атомом не обязательно приводит к ионизации. Дело в том, что наиболее часты упругие столкновения, при которых не меняется внутреннее состояние атома. Перестройка структуры атома обычно связана с возрастанием внутренней энергии атома, ее называют возбуждением атома. Атом в возбужденном состоянии находится не долго (порядка ) и затем переходит в основное состояние, излучив свет.

С ростом напряженности электрического поля, увеличивается энергия движущихся зарядов. Если она превысит энергию ионизации, то заряды будут ионизировать атомы и молекулы газа. Это механизм собственной ионизации газа, приводящий к самостоятельному разряду. Такой разряд существует  при отсутствии внешних источников ионизации.

Исследуем ионизацию и пробой в постоянном электрическом поле. Интенсивность ионизации характеризуется числом пар заряженных частиц (электронов и положительных ионов или ионов с противоположными знаками зарядов) , образуемых заряженными частицам (электронам, ионами) на единице пути их вдоль поля. Эти числа называются коэффициентами ионизации ( - для ионизации электронами и  - для ионизации ионами). Найдем связь коэффициента  с напряженностью поля.   Движение электрона приводит к развитию лавинообразной ионизации. Этот процесс грубо можно описать линейным дифференциальным уравнением для концентрации электронов

, решение этого уравнения имеет вид

.

Получим представление для коэффициента ионизации . Плотность числа пар  заряженных частиц (размерность ), порождаемых электроном на участке пути  определяется произведением вероятностей  ( - вероятность ионизации газа электроном,  - вероятность того, что электрон пройдет без столкновений расстояние в промежутке () ):