1.пробой газа, 2.поддержание полем неравновесной плазмы, 3.поддержание полем равновесной плазмы.
II) частотный диапазон поля:
1.Постоянные, низкочастотные и не слишком кратковременные импульсные поля. 2.высокочастотные поля (мегагерцовый диапазон, длины волн от метров до километров). 3.сверхвысокочастотные поля (СВЧ, гигагерцовый диапазон, длины волн от миллиметров до десятков сантиметров). 4.оптические (от далекого инфракрасного до жесткого ультрафиолетового), излучение лазеров.
Существует большое количество физических и технических применений газового разряда: ионизационная камера, фотоэлементы, счетчики с острием для измерения излучения, выпрямители (ртутные), преобразователи тока, источники света, сварочные дуги, предохранители и выключатели в электрических цепях.
15.4. Анодный ток. Нейтральные газы являются изоляторами. Если к ним приложить постоянное электрическое поле, то произойдет деформация и поворот нейтральных молекул. Поступательного перемещения молекул не будет, электрический ток не возникнет. Ситуация изменится при введении в газ посторонних (затравочных) заряженных частиц. Под действием электрического поля возникнет ток. В достаточно сильных полях будет происходить лавинообразная ионизация нейтральных молекул. Вместе с этим будет лавинообразно увеличиваться ток в газе – это и есть пример газового разряда.
Определим силу тока при движении отдельного заряда через газовый или вакуумный промежуток электрической цепи. На первый взгляд кажется, что мгновенный ток в цепи отсутствует во время движения заряда между электродами и импульс тока возникает в момент достижения зарядом электрода, когда частица передает свой заряд электроду. На самом деле это не так. Вследствие электростатической индукции на электродах наводятся заряды, и они перемещаются во внешней цепи во время движения заряда в междуэлектродном промежутке.
1). Если ![]() -
электродвижущая сила (Э.Д.С.) внешнего источника,
-
электродвижущая сила (Э.Д.С.) внешнего источника, ![]() -
тока в цепи, то работа, совершаемая этим источником за одну секунду равна
-
тока в цепи, то работа, совершаемая этим источником за одну секунду равна ![]() . Такую же работу совершает заряд
. Такую же работу совершает заряд ![]() , движущийся в поле
, движущийся в поле ![]() в вакууме со скоростью
в вакууме со скоростью ![]() , если поле
, если поле ![]() создается
этим источником (в такой задаче можно считать поле
создается
этим источником (в такой задаче можно считать поле ![]() заданным):
заданным):
![]()
и сила тока имеет представление
![]() .
.
Для
плоскопараллельных электродов задача упрощается, справедлива связь ![]() (
(![]() -
расстояние между электродами) и сила тока дается соотношением.
-
расстояние между электродами) и сила тока дается соотношением.
![]()
2).
Если в вакууме движется не одна, а много заряженных частиц, то
электрическое поле уже нельзя считать заданным. На это поле оказывает влияние
формируемый им объемный заряд. Возникает самосогласованная задача. В качестве
примера исследуем процесс в вакуумном диоде с плоскими электродами – катодом и
анодом. Пусть между этими электродами поддерживается постоянная разность
потенциалов ![]() , и нагреваемый катод непрерывно
испускает электроны. Ограничимся рассмотрением электростатического приближения,
считая эмиссию электронов постоянной. Уравнение Пуассона имеет вид
, и нагреваемый катод непрерывно
испускает электроны. Ограничимся рассмотрением электростатического приближения,
считая эмиссию электронов постоянной. Уравнение Пуассона имеет вид
![]() ,
,
где ![]() - концентрация электронов,
- концентрация электронов, ![]() . Из закона сохранения заряда в
установившемся (статическом состоянии)
. Из закона сохранения заряда в
установившемся (статическом состоянии)
![]() ,
, ![]() ,
, ![]()
следует,
что ![]() .
.
Если пренебречь диссипацией, то будем иметь закон сохранения энергии
![]() ,
,
где ![]() - масса электрона.
- масса электрона.
Из законов сохранения получаем
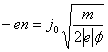
и уравнение Пуассона принимает вид нелинейного дифференциального уравнения
![]() .
. 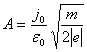 (15.1)
(15.1)
Левую часть (15.1) преобразуем
![]() ,
,
где![]() ,
, ![]() и
уравнение (15.1) после интегрирования приводится к виду
и
уравнение (15.1) после интегрирования приводится к виду
![]() ,
, ![]()
где ![]() при
при ![]() ,.
Будем считать, что на катоде выполнены условия
,.
Будем считать, что на катоде выполнены условия ![]() .
В случае
.
В случае ![]() будем иметь
будем иметь
![]() , (15.2)
, (15.2)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.