ГЛАВА 5 СИНТЕЗ ПРОГРАММИРУЕМЫХ ЛОГИЧЕСКИХ МАТРИЦ
19. Оптимизация ПЛМ по входу
Непосредственная реализация системы булевых функций. Пусть некоторая система булевых функций задана в одной из введенных ранее форм, парой матриц Х и Y, булевых или троичных. Под непосредственной реализацией этой системы (X, Y} будем понимать простейший переход от нее к структурным матрицам реализующей ее ПЛМ. Такой переход сводится обычно к простой смене интерпретации исходных матриц и не связывается с какой-либо оптимизацией.
Напомним, что структура программируемой логической матрицы представляется троичной матрицей Т (входной ступени) и булевой матрицей В (выходной ступени) и что функциональные свойства ПЛМ описываются уравнением
Y = ┐ В^ ┐ Т^Х = ┐ B\УT^ ; X,
задающим выходную информационную матрицу Y как функцию входной информационной матрицы X.
Если система булевых функций задана булевой матрицей X, в которой перечислены (столбцами) некоторые наборы значений аргументов, и булевой матрицей Y, где аналогичным образом представлены соответствующие значения функций системы, то непосредственная реализация заключается в том, что в качестве структурной троичной матрицы Т принимается X7 (инверсированная и транспонированная матрица X), а в качестве структурной матрицы В — матрица У.
Например, если
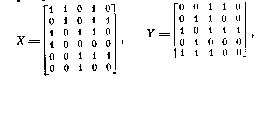 |
|
то структурные ственно систему - |
|
|
|
матрицы ПЛМ, реализующей непосред(X, Y), имеют следующий вид: |
Схема соответствующей ПЛМ приведена на рис. 49. На рис. 50 показана эквивалентная ей двухъярусная схема, реализующая композицию из конъюнктивного и
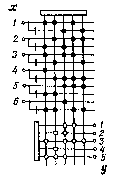 |
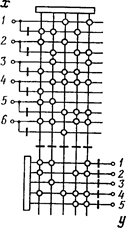
Рис. 49. Непосредственная реализация па ПЛМ системы булевых функций, заданных поэлементно.
Рис. 50. Двухъярусная схема из конъюнктивного и дизъюнктивного матричных операторов, эквивалентная предыдущей (см. рис. 49).
дизъюнктивного матричных операторов. Такая схема более удобна, поскольку ее построение не связывается с ин-версированием матриц Х и Y. Схемами такого рода мы и будем пользоваться в дальнейшем, имея в виду, что переход от них к ПЛМ элементарен.
Совершенно так же производится непосредственная реализация системы булевых функций и в более общем случае, когда система задана троичной матрицей X, пере
числяющей некоторые элементарные конъюнкции, и булевой матрицей Y, где единицами отмечены те из них, которые входят в соответствующие дизъюнктивные нормальные формы.
Непосредственная реализация заданной системы булевых функций оказывается весьма простой. Трудности возникают при поиске оптимальной схемы. Сведем решение этой задачи к оптимизации исходной системы (X, Y).
Не теряя общности рассуждений, будем пока считать, что исходная, подлежащая реализации система F состоит из частичных булевых функций f1,f2,…,fmзадана парой булевых матриц Х и Y. Будем говорить, что некоторая другая система G, состоящая из булевых функций g1,g2,…,gm реализует систему F, если каждая из функций системы F реализуется соответствующей функцией из системы G. Определим оптимизацию системы F как нахождение такой простейшей пары из троичной матрицы X* и булевой матрицы Y*, задаваемая которой в дизъюнктивной нормальной форме система булевых функций реализует систему F.
Простота находимого решения оценивается прежде всего размерами матриц X* и Y*, определяющими площадь ПЛМ, реализующей непосредственно систему (X*, Y*). Дополнительным критерием оптимизации может служить число единиц в матрице Y* и общее число единиц и нулей в матрице X*. Эти величины задают число транзисторов в ПЛМ.
Знакомство с общей проблемой синтеза оптимальных ПЛМ начнем с рассмотрения задачи оптимизации ПЛМ по входу, когда в качестве матрицы Y* принимается без изменений исходная матрица Y и трансформациям подвергается лишь входная матрица X. Прежде всего попытаемся минимизировать число строк в матрице X*, поскольку число столбцов в ней зафиксировано — оно равно числу столбцов в матрице Y.
Классификация аргументов частичных функций. Рассматривая некоторую полностью определенную булеву функцию
f (х1,x2,…,xn), всегда можно однозначно разбить множество ее аргументов на два класса, включив в один из них действительные аргументы, от которых функция действительно зависит, и образовав другой класс из фиктивных аргументов, изме-
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.