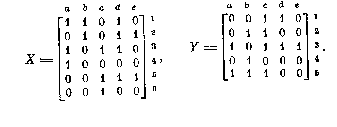
Математика \ Дискретная математика

Синтез программируемых логических матриц. Оптимизация ПЛМ по входу. Классификация аргументов частичных функций, страница 5


Построим

матрицу Z, отметив

ее строки соответствующими литералами :


Анализируя

матрицу

Y, замечаем

, что

Большинство

упорядоченных пар ее столбцов находится в отношении превышения. Исключение составляют пары (а, с), {d, с), (е, а), (е, с) и(е, d). Получим матрицу превышений, отмечая ее столбцы парами орождающих их столбцов матрицы Z:




Для нахождения кратчайшего строчного покрытия этой матрицы применим метод редуцирования, последовательно удаляя то поглощающие столбцы, то поглощаемые строки. В результате матрица упрощается до следующего не редуцируемого далее минора:


Проведем расщепление возникшей критической ситуации по первому столбцу.

Выберем сначала строку 3. Тогда процесс редуцирования возобновляется и доходит до получения строчного покрытия (2, 3, 1`, 5'), которому соответствует совокупность литералов (х2,х3,x`1,x`5), задающая следующую реализацию исходной системы:


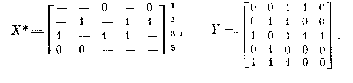
Рассмотрение другого варианта, связанного с выбором строки 2', приводит к получению ра} неценного решения (x1, x5,x`1,x`5), задающего следующую реализацию :




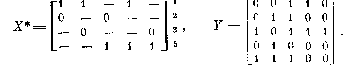
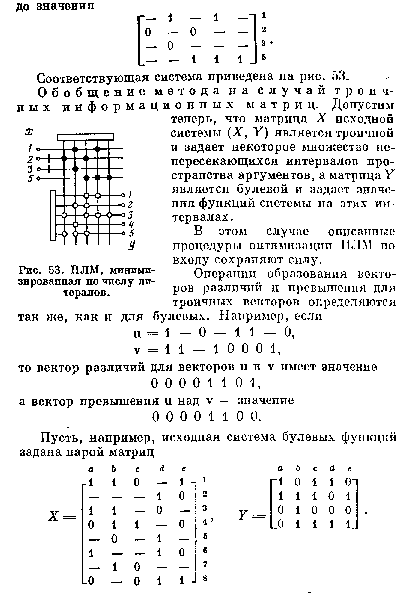В силу достаточности выполненною перебора вариантов при поиске кратчайшего покрытия матрицы оба решения являются оптимальными. Однако при дополнительной оптимизации по числу транзисторов второй вариант приводит к лучшему результату. Матрица X* сокращается


231


ГЛ. 5. СИНТЕЗ ПЛМ

минора матрицы X:


в котором значения элементов x8d и x8b заменены на «—»,

поскольку  литерал  х8  не вошел в решение.Для каждого из столбцов

этого минора строится матрица различий с теми столбцами матрицы  Х,

которым он должен остаться ортогональным :


Кратчайшие строчные покрытия этих матриц находятся элементарным  образом .

Элементы  матрицы  Х*, соответствующие входящим в полученные покрытия строкам

сохраняют  свои значения , приобретают значение «— ».В результате получаем

оптимальную реализующую систему

               
20. МИНИМИЗАЦИЯ СИСТЕМЫ БУЛЕВЫХ ФУНКЦИЙ   233

          20. Минимизация системы булевых функций

Нахождение кратчайшей ДНФ системы булевых функций. Существенным параметром, определяющим сложность ПЛМ, является число I промежуточных переменных z1, z2, . . ., zi, представляющих состояния выходных полюсов первой ступени, равное числу непосредственно соединенных с ними входных полюсов второй ступени. Другими словами, этот параметр задает число строк в структурной матрице Т и число столбцов в матрице В. Минимизация этого параметра при синтезе ПЛМ, реализующей некоторую заданную систему булевых функций, является достаточно сложной задачей теории булевых функций, известной под названием задачи совместной минимизации системы булевых функций в классе дизъюнктивных нормальных форм, а точнее говоря, получения кратчайшей ДНФ для системы булевых функций. Минимизируется в этом случае общее число различных элементарных конъюнкций, из которых образуются Д11Ф, представляющие булевы функции заданной системы.

Пусть исходная система F состоит из частичных булевых функций fi (здесь, как и далее, пробегает значения 1, 2, . . ., т), заданных соответственно характеристическими множествами М1i и М°i, представляющими собой некоторые подмножества общего булева пространства М.Очевидно, что получение кратчайшей ДНФ системы F сводится к нахождению такого минимального множества интервалов пространства М, чтобы каждое из множеств М1i покрывалось совокупностью тех из них, которые нс пересекаются соответственно с множеством М°i.

Точное решение этой задачи может быть получено следующим методом.

Рассмотрим бинарное отношение принадлежности элементов пространства М множествам М1i, представляющее собой множество Р всех пар типа (тj, k), где тj — элемент булева пространства М, принадлежащий в то же время множеству M1k, помер которого задан вторым элементом пары (mj,k). Назовем некоторое подмножество из Р интервалъно-поглощаемым, если существует такой интервал множества М, который для каждой пары (mj,k), принадлежащей данному подмножеству, содержит элемент тj и не

Скачать файл