нение значений которых не может привести к изменению значения функции. Будем считать, что фиктивные аргументы можно вообще удалить из множества {x1,x2,…,xn}, сократив соответственно размерность булева пространства аргументов, и что функция f остается при этом прежней. Однако чаще всего класс фиктивных аргументов оказывается пустым.
В случае частичных булевых функций мы встречаемся с принципиально иной ситуацией. Здесь также можно иногда найти действительные аргументы, но (если только множество М‾ не пусто) нельзя найти аргументы, фиктивные в строгом смысле этого слова. Зато могут встретиться такие аргументы, которые нельзя отнести ни к действительным, ни к фиктивным. Дело в том, что при одном доопределении рассматриваемой частичной функции они окажутся действительными, а при другом — фиктивными. Назовем их возможными аргументами.
С ростом неопределенности булевой функции растет и доля возможных аргументов. Слабо определенные функции имеют, как правило, лишь возможные аргументы. В самом деле, функция обладает действительными аргументами лишь тогда, когда существует хотя бы одна пара соседних наборов, на одном из которых функция принимает значение 0, а на другом — значение 1. Вероятность такого события для слабо определенных булевых функций мала.
С аналогичной ситуацией мы будем иметь дело и при рассмотрении системы частичных булевых функций, заданной входной булевой матрицей Х и соответствующей ей выходной матрицей Y.
Пусть, например,
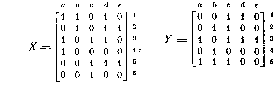 |
Любой из шести аргументов х1,x2,…,x6 является здесь лишь возможным. При некотором доопределении системы он становится фиктивным и, следовательно, может быть удален из множества аргументов. При этом выбрасывается соответствующая строка в матрице Х и получается другая система частичных 'булевых функций, реализующая заданную систему. Но это не значит, что из рассматриваемой системы можно удалить сразу все аргументы.
|
Х*== 1 |
|
Y |
Например, из матрицы Х можно выбросить строку 1, что соответствует такому доопределению системы, при котором фиктивным становится аргумент х1. В получаемой при этом системе
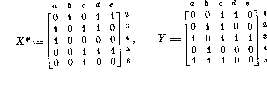
оказываются два соседних набора d и е, на которых принимает различные значения выходная переменная У1 Это значит, что аргумент Х3, по которому наборы ортогональны оказывается теперь действительным и уже не может-
быть исключен из системы.
Минимизация ч и с л а аргументов в реализующей системе. Представляет интерес задача минимизации числа аргументов в системе частичных булевых функций, т. е. нахождение такой системы, которая будет реализовывать заданную систему, обладая минимальным числом аргументов. Очевидно, что эта система должна быть получена путем такого доопределения заданной системы, при котором как можно больше аргументов становятся фиктивными и выбрасываются из множества аргументов.
Одна из практических интерпретации данной задачи заключается в минимизации числа входных полюсов ПЛМ, равного числу столбцов во входной транзисторной матрице этой схемы, реализующей заданную систему частичных булевых функций.
Выбрасывая из заданной системы некоторые аргументы и удаляя соответствующие строки в матрице X, необходимо следить за тем, чтобы не получить на некотором шаге такой остаток матрицы X, в котором окажутся равные между собой столбцы, соответствующие столбцам матрицы Y с различными значениями. Это значит, что решаемая задача по существу совпадает с задачей нахождения теста для булевой матрицы X, уточняясь следующим образом: для заданной пары булевых матриц Х uY с одинаковым числом столбцов найти в матрице Х минимальную совокупность строк, образующую минор, в котором любая пара столбцов, соответствующая столбцам матрицы Y с различными значениями, также будет иметь различные значения.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.