Синтез программируемых логических матриц. Оптимизация ПЛМ по входу. Классификация аргументов частичных функций, страница 3

Поэтому, решая задачу минимизации числа аргументов, найдем в матрице Y все пары столбцов с различными значениями, построим векторы различий для соответствующих им пар столбцов матрицы Х (они получаются покомпонентной операцией дизъюнкции с исключением), составим из этих вектор столбцов булеву матрицу различий и найдем ее кратчайшее строчное покрытие. Совокупность строк матрицы X, соответствующих элементам найденного покрытия, представит решение данной задачи.

Поскольку в рассматриваемом примере все столбцы матрицы Y оказываются различными, векторы различий строятся в данном случае для всех десяти пар столбцов матрицы X. В результате получим следующую булеву матрицу различий, столбцы которой отмечены сверху порождающими их парами столбцов матрицы X:

Легко убедиться					в	отсутствии	двухэлементных покрытий этой матрицы
	и	в	том,	что одним из строчных покрытий ее служит совокупность первых
	трех строк. Следовательно, задача в имеет оптимальное решение

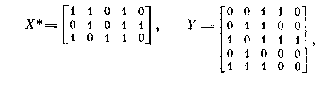
которое можно рассматривать как сжатую форму следующего доопределения исходной системы (X, У), где число наборов, на которых определены значения выходных переменных, увеличено в восемь раз:

Непосредственная реализация полученной системы

(X*, У) показана        на рис. 51.

Решая данную задачу для более сложных систем частичных булевых функций, описываемых многостолбцовыми матрицами Х и Y, можно пользоваться приближенными метода        ми поиска минимальных тестов.

Сокращение    числа транзисторов.

Анализируя синтезированную схему, можно убедиться в ее избыточности, заключающейся в том, что при удалении некоторых транзисторов она по-прежнему будет реализовывать исходную систему (X, Y}.Возникает задача максимального упрощения схемы, при котором в ней останется минимальное число транзисторов. Удалению транзисторов соответствует замена значений 0 или 1 соответствующих элементов матрицы X* на значение «—», а это изменение в свою очередь, интерпретируется как расширение интервалов, на которых соответствующими столбцами матрицы У заданы значения выходных переменных.

Очевидно, что если сокращение числа единиц и нулей в матрице X* проводится таким образом, что ее столбцы остаются взаимно ортогональными, то получаемая при этом система будет по-прежнему реализовывать исходную систему (X,Y). Действительно, если ПЛМ реализует непосредственно исходную систему (X, У), то ее промежуточные переменные z1, z2, . . ., z', характеризующие состояния выходных полюсов первой ступени, поставлены во взаимно однозначное соответствие; с наборами значений аргументов, на которых определены булевы функции исходной системы. При подаче на вход ПЛМ одного из этих наборов, представленного некоторым вектор столбцом х^˜ входной информационной матрицы X, значение 1 принимает соответственно переменная zi, и только она, инициируя отображение на выход схемы соответствующего столбца матрицы Y. Эта ситуация не будет меняться при замене наборов на поглощающие их интервалы, если эти интервалы не пересекаются.

Однако данное требование не является необходимым. Во-первых, можно допустить пересечение интервалов за пределами области определения исходных частичных булевых функций. Во-вторых, при определенных условиях интервалы могут пересекаться и на этой области.

Необходимое требование к системе (X*, У), реализующей систему (X, У), формулируется следующим образом:

i-й столбец матрицы X* должен быть ортогонален j-му столбцу матрицы X, если i-й столбец матрицы У не поглощается ее j-м столбцом.