Например, в полученной паре матриц X* и У столбец 1 матрицы У поглощается лишь столбцом 3, откуда следует, что столбец 1 матрицы X* должен быть ортогонален столбцам 2, 4 и 5 матрицы X. Для выполнения этого условия необходимо и достаточно оставить в этом столбце лишь значение х12= 0, заменив остальные значения на «—». Второй столбец матрицы X* обязан оставаться ортогональным всем столбцам матрицы X, и это требование обеспечивается сохранением значений элементов х21= 1 и x23, = 0; элемент х22 получает при этом значение «—». Аналогично проводится сокращение числа единиц и нулей в столбцах 3 и 4. Наконец, столбец 5 матрицы У не поглощается лишь столбцом 2. В соответствии с этим необходимо сохранить значение элемента x15= 0. В итоге число единиц и нулей в матрице X* минимизируется и реализующая система (X*, Y) принимает значение
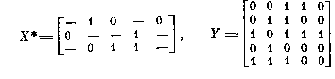
|
|
|
Рпс. 52. ПЛМ, минимизированная по числу транзисторов. |
Соответствующая схема приведена на рис. 52. В рассмотренном примере минимизация числа единиц и пулей в матрице X* прошла легко. В более сложных ситуациях задача решается путем построения для каждого столбца упрощаемой матрицы X* булевой матрицы отношения его различий с теми из столбцов матрицы X, с которыми он должен оставаться ортогональным, и нахождения кратчайшего строчного покрытия этой матрицы. Следует затем сохранить значения рассматриваемого столбца в тех строках, которые войдут в найденное покрытие, и присвоить остальным компонентам столбца значение «—». Так находится оптимальное решение.
Минимизация числа литералов. Если реализуемая программируемой логической матрицей система булевых функций от п переменных оказывается монотонной, то число столбцов во входной транзисторной матрице равно n. В общем же случае это число может достигать значения 2n. При этом произвольная система функций как бы сводится к монотонной путем удвоения числа аргументов, при котором множество аргументов х1,x2,…,xn заменяется на новое множество аргументов x1,x2,…,xn, x`1,x`2,…,x`n
рассматриваемых условно как независимые. Будем называть эти аргументы литералами. Именно им и соответствуют столбцы входной транзисторной матрицы.
Уточним в связи с этим задачу минимизации числа столбцов во входной транзисторной матрице как задачу минимизации числа литералов в заданной системе частичных булевых функций.
Рассматривая равные по длине булевы векторы а и b, будем говорить, что вектор а превышает вектор b, если и только если в них существует некоторая пара одноименных компонент ai, и bi, со значениями ai = 1 и bi= 0.
Введем в рассмотрение булев вектор превышения вектора а над вектором b, полагая, что он принимает значение 1 в тех и только тех компонентах, которым соответствуют значения аi= 1 и bi = 0.
Удвоение числа аргументов в системе сопроводим удвоением числа строк в матрице X, введя туда дополнительно инверсные значения для всех уже существующих строк. Полученную матрицу, строки которой соответствуют литералам исходной системы, обозначим через Z. Каждой упорядоченной паре (zi,zj) столбцов этой матрицы соответствует свой вектор превышения. Будем считать что он задает стандартным образом некоторое подмножество из множества всех литералов, п назовем это подмножество множеством превышения zi над zj
В основе излагаемого ниже метода минимизации числа литералов лежат следующие два утверждения.
Если некоторый столбец у1 матрицы yj превышает столбец у , то в число литералов реализующей системы должен войти по крайней мере один из элементов множества превышения zi надzj.
Совокупность необходимых условий данного типа, находимая путем рассмотрения всех пар столбцов матрицы У, находящихся в отношении превышения, образует достаточное условие реализуемости.
Эти утверждения позволяют свести рассматриваемую задачу, подобно предыдущим, к нахождению кратчайшего покрытия некоторой булевой матрицы, на этот раз — матрицы превышений, образуемой вектор-столбцами превышений для тех упорядоченных пар столбцов матрицы Z, которые соответствуют находящимся в отношении превышения столбцам матрицы Y.
Вернемся к старому примеру. Пусть
8*
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.