Нахождение ядра безъизбыточной ДНФ
Пусть задана ![]() -переменные
образуют вектор x_
-переменные
образуют вектор x_
{P1,P2,P3,…,Pk)=P*
k- число без избыточных импликант .
Возьмем пересечение ∩[P*] .Получим множество импликант ,
содержащихся в каждой ДНФ.
∩[P*] — ядро.
Ядро можно найти даже не строя множество всех простых импликант .
Найдем произвольную одну СДНФ , а потом распознаем ядро.
Д=k1√k2√…√km.
т.е. должен быть определен элемент
Нам даны интервалы , образуемые нашей СДНФ.
![]()
![]() f
f
![]() e
e
![]()
![]() d
d
|
1 |
1 |
||||||
|
|
1 |
1 |
|||||
|
|
1 |
1 |
|||||
|
1 |
1 |
||||||
|
|
1 |
1 |
1 |
||||
|
|
1 |
1 |
|||||
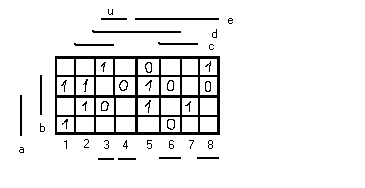
a b c
Выделенные элементы не являются элементами ядра.
Перейдем к более общей форме
a b c d e f
┌- 1 0 0 1 -┐
│0 1 - - 1 1│
│0 - 1 - 0 1│
│0 0 0 1 - 1│
└ ┘
Среди всех строк выбираем неортогональные (пересек.) или ортоганальные
По одной компоненте (смежные).
Рассмотрим 1 : 2 a f
0 1 — множество элементов не являются обязательными для 2 : c d
0 0 —матрица вырожденная так как нет вектора,
1 - ортоганального каждой строке
0 1
для 3 : b d
1 - — есть ортогональный вектор [0 0]
0 1 т.е. решение для 4 : e
1 вырожденная
0
![]() — обязательные
— обязательные
Декомпозиция булевых функций.
где x = u È v , u Ù v = Æ
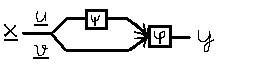
Декомпозиция - процесс получения композиции.
существуют ли такие ф-ции j и y.
Для удобства : y = j(z,v) z = y(u).
Рассм. нашу ф-цию :
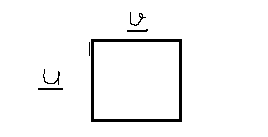
В завис. от u получим j(0,v) = j v (v) или
j(1,v) = j 1 (v)
j 0 , j 1 – в таблице представл. строкой . Если в таблице будет больше двух строк, то ф-ция не разделима на j и y.
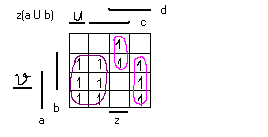
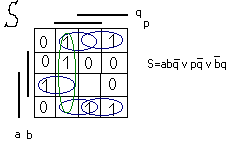
Пусть
задана ф-ция.
Существует только 2 типа столбцов.
z = cd = y(c,d)
_ _
y = j(z,a,b) = za È z(a È b)
Рассмотрим част. опред. ф-цию.
Нужно
дополнить таблицу так, чтобы было 2 типа столбцов.
Если вектора уже ортогональны, то их дополн. не нужно, а искать другое.
Столбец 1: ортоганален 4,6,8. Строим граф ортогональности. Если он бихроматичен, т.е. можно раскрасить двумя красками, то решение есть.
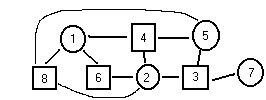
Все циклы чётные, то граф бихроматичен.
y![]()
![]()
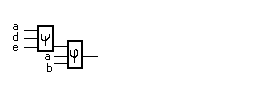
=
de È de È cde
_ _ _
j =za bÈz(aÈb)
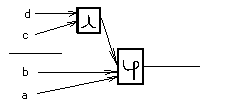
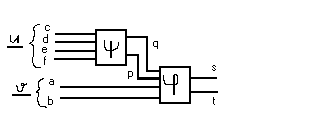
Декомпомпозиция системы булевых функций.
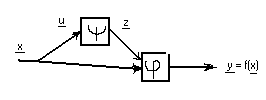
y = j(y(u),v) x = u È v; u Ç v=Æ
Рассм. два значения вектора x.
xi , xj Допустим, что им соответствуют
yi , yj различные значения вектора y.
yi = f( xi ); yj = f( xj ) yi ¹ yj
Так же будут различатся значения на входе j.
Если вектора xi и xj не различ. по v то различ. по z.
Т.е. если (yi ¹ yj) Ù (vi = vj ) ® (zi ¹ zj ) z = y(u).
v u y
_____ab______cdef________st___________
00 1011 1 00 00
00 0010 2 11 10
00 0001 3 10 01
01 0010 2 10 10
01 1011 1 00 00
01 1010 4 00 11
01 1100 5 01 01
10 1011 1 01 00
10 0110 6 01 00
10 1100 5 10 01
10 1010 4 10 11
11 1110 7 00 01
11 0110 6 11 00
Построим граф различпости.
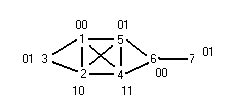
y
cdef pq
1011 00
0010 10
0001 01
1010 11
1100 01
0110 00
1110 01
j
abpq st
0000 00
0010 11
0001 10
0110 11
0100 00
0111 00
0101 01
1000 01
1001 10
1011 10
1101
 00
00
1100 11
Обычно задача минимизации общего числа конъюнкций системы ДНФ, реализующих булеву функцию.
В общем случае система частично определенных булевых функций.
Х-мн-во булевых функций.
М-булеан множества Х(мн-во векторов)
Множество векторов т задает бул.пр-во 2n
Md – область определения бул. функций(Md <=M)
a b c d e f u v w
1 1 0 0 1 0 1 1 0 0 на остальных наборах функции не
2 0 1 0 1 1 0 0 0 1 определены
3 1 1 1 0 0 1 0 1 0
4 0 1 0 1 0 1 1 1 0
5 1 0 1 1 0 1 1 1 0
6 0 0 1 0 1 1 0 1 1
7 0 1 1 0 0 0 0 1 1
8 0 1 1 0 1 1 1 1 1
![]()
![]() из 6,7,8 строки смотрим по функциям и видим что у
двух последних на этих векторах
единицы поэтому 0 - 1 0 - - т.е. a
c d (*)
из 6,7,8 строки смотрим по функциям и видим что у
двух последних на этих векторах
единицы поэтому 0 - 1 0 - - т.е. a
c d (*)
Решение: _
a b c d e f u v w U=abf v de
0 1 - - - 1 1 1 0 _
- - - 1 0 - 1 0 0 V=abf v c
- - 1 - - - 0 1 0 _
- - - - 1 - 0 0 1 W=e v f
- - - - - 0 0 0 1
Точный метод:
Покрытие R правильными минорами(всовокупность единичных значений на пересечении строк и столбцов)
Правильный минор-единичный минор удовлетворяющий условию:все функции должны соответствовать столбцам этого минора.
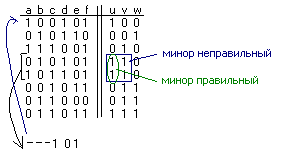 Смотрим
какие элементы попадают в * -таких элементов нет поэтому эту элементарную
конъюнкцию можем внести в ДНФ каждой функции.
Смотрим
какие элементы попадают в * -таких элементов нет поэтому эту элементарную
конъюнкцию можем внести в ДНФ каждой функции.
Задача:
Найти все правильные миноры и ими покрываем R (матрицу связи)
Максимальные правильные миноры –не содержатся в других правильных минорах.
Матрица правильных миноров:
1 2 3 4 5 6 7 8 u v w
0 0 0 1 0 0 0 1 1 1 0 1
0 0 0 0 0 1 1 1 0 1 1 2
1 0 0 1 1 0 0 0 1 0 0 3
0 0 1 0 1 1 1 1 0 1 0 4
0 0 1 1 0 0 1 0 0 1 0 5
0 0 0 1 0 1 0 1 0 1 0 6
0 1 0 0 0 1 0 1 0 0 1 7
0 1 0 0 0 0 1 0 0 0 1 8
0 0 0 0 0 0 0 1 1 1 1 9
0 0 0 0 1 0 0 0 1 1 0 10
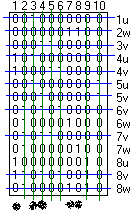 минимизируем
количество столбцов, покрывающих все строки
минимизируем
количество столбцов, покрывающих все строки
Матрица элементарных конъюнкций:
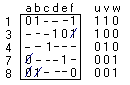 Минимизируем
литералы: литерал можно выбросить если этот интервал не входит в
другие интервалы.
Минимизируем
литералы: литерал можно выбросить если этот интервал не входит в
другие интервалы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.