










рицы Y и, следовательно, исчезновение любой единицы в матрице В автоматически влечет за собой исчезновение соответствующей единицы в матрице Y. Связь единиц можно показать, обозначив их, как это показано ниже:
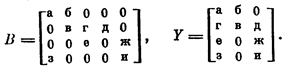 |
Очевидно, зная это соответствие, можно легко распознать любую кратную неисправность в рассматриваемой матрице В.
Приближенный метод. Приведенная интерпретация показывает, что задача сводится к некоторой упаковке единиц матрицы В в матрицу Y. Развивая эту идею, предложим другой метод решения задачи, быстрее ведущий к цели, хотя и не гарантирующий минимальность получаемого решения.
Отличие предлагаемого метода от предыдущего заключается в том, что мы обходимся теперь без построения
|
Рис. 35. Граф несовместимости столбцов исходной матрицы В. |
матрицы требований R, а получаем граф а получаем граф несовместимости непосредственно для столбцов исходной матрицы В, полагая при этом два столбца несовместимыми, если они имеют значение 1 в некоторой одноименной компоненте, т. е. если их конъюнкция отлична от нуля. Построенный таким образом граф, соответствующий рассматриваемому примеру, показан на рис. 35.
Нахождение минимальной раскраски этого графа проще, поскольку он меньше предыдущего. Легко находится одно из решений — разбиение {о, с / b, e / d}. Столбцы матрицы Х представляют непосредственно классы этого разбиения:
Соответствие между единицами матрицы В и единицами матрицы Y будет иметь теперь следующий вид:
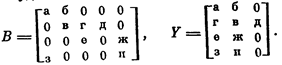 |
 |
Однако для каждой конкретной троичной матрицы Т можно найти конкретное решение — входную матрицу Х с минимальным числом столбцов, позволяющую распознать любую кратную неисправность обсматриваемого класса.
Хотя в данном случае выход из строя некоторого транзистора интерпретируется на троичной матрице иначе чем на двоичной, а именно заменой значения 0 или 1 некоторого элемента матрицы на «-», требование, предъявляемое к матрице X, формулируется аналогично тому, как это делалось ранее.
Пусть, например (рис. 36),
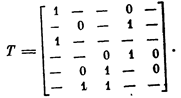 |
Выход, из строя верхнего левого транзистора в схеме представляется сменой значения элемента t11 с 1 на «—». Обнаружить эту неисправность можно таким и только таким входным набором х1 в котором x11 =1 и x14=1. Соответствующее требование к матрице Х представляется вектором 1 — — 1 —, включаемым в матрицу требований R в качестве ее столбца. Находя таким же образом остальные требования (число их равно числу транзисторов в схеме, или общему числу нулей и единиц в матрице Т), мы формируем матрицу требований

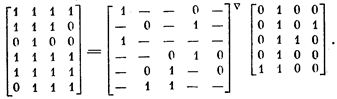
Далее задача решается совершенно так же, как и при рассмотрении уравнения Y = ВvХ. Совмещение столбцов матрицы R приводит нас к искомой матрице X:
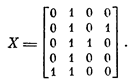 |
 |
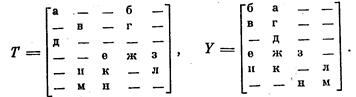 |
Отмеченные элементы полностью представляют своими значениями состояние диагностируемой матрицы: если некоторый из них имеет значение 1, это означает, что соответствующий ему транзистор на месте, значение 0 указывает на исчезновение транзистора. Значения остальных элементов, показанных в матрице символом «—», могут при этом не приниматься во внимание.
11. Нахождение минимального дизъюнктивного базиса
Минимальный дизъюнктивный базис для матрицы Y и ее кратчайшее минорное покрытие. Пусть булевой матрицей Y' (ее столбцами) задано некоторое множество булевых векторов и требуется построить схему, для которой эти векторы были бы выходными. Такую схему всегда можно найти среди транзисторных матриц. Естественно потребовать, чтобы она была простейшей, т. е. обладала бы минимальным числом столбцов (число ее строк определено заранее — оно равно числу строк матрицы Y'). Нужно также найти входные векторы, преобразуемые синтезируемой матричной схемой в заданные выходные, и представить их множество как множество столбцов булевой матрицы X.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.