Нахождение минимального дизъюнктивного базиса, страница 3

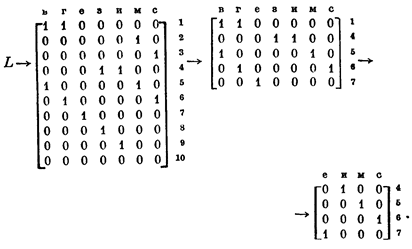
Допустим, например, что то m£n (принципиального значения это условие не имеет) и мы перебираем подмножества строк матрицы Y, представляя их значениями характеристического вектор-столбца р, единицы в котором соответствуют строкам, вошедшим в рассматриваемое подмножество Р. Покомпонентную конъюнкцию выбранных строк представим вектором q = /\ [Р], задающим некоторое подмножество столбцов Q. Рассмотрим минор матрицы Y, образуемый пересечением элементов из множеств Р -в. Q, представляемых характеристическими векторами р и q. Он будет единственным максимальным единичным минором, соответствующим множеству Р, если только в матрице Y не существует такой строки у_i которая не принадлежала бы множеству Р и для которой выполнялось бы отношение q£ у_i. Если же такая строка существует, то минор можно распространить на нее, т. е. очевидно, что в этом случае он не будет максимальным.

Отсюда вытекает справедливость следующего утверждения. Множество максимальных единичных миноров булевой матрицы Y находится во взаимно однозначном соответствии с множеством таких подмножеств Р множества строк матрицы Y, для которых выполняется условие:

где р — характеристический вектор множества Р, а q — характеристический вектор соответствующего ему подмножества столбцов Q.

Не останавливаясь здесь на том, как производится перебор на множестве строк при поиске подмножеств с отмеченным свойством (перебор может вестись по-разному), представим результат, получаемый для рассматриваемого конкретного примера, в форме булевой матрицы, столбцы которой задают все интересующие нас значения характеристического вектора р:

Далее введем следующим образом индивидуальные имена для единичных элементов матрицы Y:

~ 1	1	1	о'
о	о	о	1
1	о	о	о
(1	1	о	1
u	о	1	i,

В результате становится очевидным, что решение образуется четырьмя минорами с номерами 4, 5, 6 и 7. Соответствующие им значения характеристического вектора р рассматриваются как столбцыb^k искомой матрицы В, а соответствующие значения характеристического вектора q (q == /\ [P]) — как строки x_k искомой матрицы X:

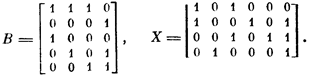Редуцирование матрицы Y. При большом числе единичных элементов в матрице Y описанный метод, связанный с построением и последующим редуцированием матрицы L, становится весьма трудоемким. Между тем редуцирование матрицы L можно заменить соответствующим редуцированием исходной матрицы У. Установим характер этого соответствия.

Будем говорить, что элемент y^j_i матрицы Y мажорирует элемент y^l_k этой же матрицы, если второй из них принадлежит любому максимальному единичному минору, которому принадлежит первый. Соответствующие этим элементам столбцы матрицы L будут находиться в отношении поглощения: столбец, соответствующий элементу у^l_k будет поглощать столбец, соответствующий элементу y^j_i.Если будет обеспечено покрытие элемента y^j_i некоторым максимальным единичным минором, то о покрытии элемента y^l_k можно не беспокоиться — он будет покрыт «автоматически».