Нахождение минимального дизъюнктивного базиса, страница 2

Другими словами, требуется найти булеву матрицу В с минимальным числом столбцов и булеву матрицу Х с таким же числом строк, удовлетворяющие уравнению Y' = Вv Х при заданной булевой матрице Y'.

Заменив матрицу Y' ее отрицанием Y = Y', перейдем к рассмотрению уравнения Y = ВvХ с заданной матрицей Y и искомыми матрицами В и X.

Каждый столбец матрицы Y равен дизъюнкции некоторых столбцов матрицы B (каких именно, показывается единицами в соответствующем столбце матрицы X). Поэтому рассматриваемая задача сводится к нахождению такого множества вектор-столбцов, которое позволило бы сформировать посредством операции дизъюнкции любой из столбцов матрицы У. Назовем это множество дизъюнктивным базисом (для столбцов матрицы У) и сформулируем задачу следующим образом.

Для заданной булевой матрицы У найти булеву матрицу В с минимальным числом столбцов, причем такую, что каждый столбец матрицы У будет равен покомпонентной дизъюнкции некоторых столбцов матрицы В.

Последующий поиск матрицы X, удовлетворяющей уравнению У = ВvХ, где заданы уже две матрицы У и В, представляет собой более простую задачу, которая нами уже рассматривалась.

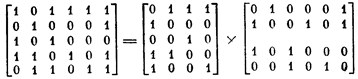
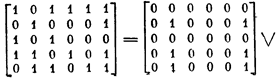
Возможен и другой подход к решению поставленной задачи, при котором матрицы В и Х ищутся одновременно. Вспомним, что уравнение У == ВvХ по определению эквивалентно уравнению У = В´ X, т. е.

откуда следует, что матрицу У можно представить как покомпонентную дизъюнкцию матриц

Например, следующее произведение конкретных  булевых матриц представляется покомпонентной матричной дизъюнкцией

Каждый из членов этой дизъюнкции — произведение вектор-столбца b^k на вектор-строку x_k — представляет собой булеву матрицу, единичные элементы которой образуют минор, и этот минор задается пересечением тех строк и столбцов матрицы У, соответствующие которым компоненты векторов b^k иx_k обладают значением 1.

Отсюда следует, что решение рассматриваемой задачи можно свести к нахождению минимальной системы единичных (не содержащих нулей) миноров заданной матрицы У, покрывающих совместно все единицы этой матрицы: каждая из этих единиц должна принадлежать хотя бы одному из найденных миноров. Учитывая данную интерпретацию, решаемую задачу можно назвать задачей о кратчайшем минорном покрытии булевой матрицы У.

Прямой  метод  нахождения кратчайшего   минорного   п о к р ы т и я. Но трудно показать, что если ищется только одно из кратчайших минорных покрытий, то можно ограничиться рассмотрением максимальных единичных миноров матрицы У, т. е. таких, которые не содержатся в других единичных минорах. Действительно, если существует такое кратчайшее минорное покрытие, некоторые элементы которого представляют собой единичные миноры, не являющиеся максимальными для данной матрицы У, то их можно заменить на соответствующие максимальные, в которых они содержатся, и получить таким образом минорное покрытие, которое также будет кратчайшим.

Следовательно, решение сформулированной задачи можно свести к получению всех максимальных единичных миноров матрицы У, построению булевой матрицы отношения принадлежности им единичных элементов матрицы Y (допустим, что эти элементы будут представляться столбцами матрицы отношения) и нахождению ее кратчайшего строчного покрытия. Назовем этот метод прямым.

Общее число миноров матрицы размером m на n равно 2^m+n, однако при поиске максимальных единичных миноров незачем их все перебирать. Достаточно организовать перебор подмножеств строк или подмножеств столбцов, выбрав при этом меньшее из чисел тип. Каждому из этих подмножеств будет соответствовать не более одного максимального единичного минора.