Нахождение минимального дизъюнктивного базиса, страница 6

Здесь в качестве определяющих можно выбрать элементы б и д; каждый из остальных элементов совместим с каким-либо из них.

Каждый из определяющих элементов, выбранных нами, однозначно определяет некоторое максимальное совместимое подмножество из множества единичных элементов текущего значения матрицы Y*. Для этого подмножества находится (в общем случае уже неоднозначно) некоторый максимальный единичный минор матрицы Y, вводимый в решение. Представляя эти миноры парами «столбец матрицы В — строка матрицы X», мы находим матрицы В и X:

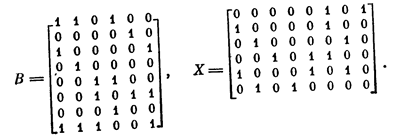Решение совпадает (с точностью до перестановки столбцов в В и строк в X) с полученным ранее.

Заключительные замечания. Конечно, далеко не всегда рассматриваемая задача может быть решена только редуцированием исходной матрицы Y и последующим конструированием решения путем нахождения определяющих элементов. В общем случае эти операции следует чередовать с расщеплением некоторых ситуаций, т. е. с организацией некоторого перебора вариантов построения решения, гарантирующего получение кратчайшего минорного покрытия. Как и в предыдущих задачах, усилия здесь должны направляться главным образом на сокращение возникающего перебора. В данном случае они могут найти выражение в поиске таких существенных элементов, которые входят в минимальное число максимальных совместимых подмножеств, и рассмотрении последних по очереди.

Отказавшись от гарантии минимальности получаемого минорного покрытия, можно значительно сократить время, затрачиваемое на его конструирование, выбирая в критических ситуациях, когда матрица У* далее не редуцируется и определяющих элементов в ней не находится, наиболее перспективный вариант продолжения процесса конструирования.

Реализуемый при этом шаг можно определить следующим образом: найти такой существенный элемент в матрице У*, который принадлежит минимальному числу максимальных совместимых подмножеств, выбрать среди последних такое, которое содержит максимальное число существенных элементов, найти для него некоторый содержащий его максимальный единичный минор матрицы Y и включить этот минор в решение.

Заметим, что исследованная нами задача оказывается равносильной следующей: найти простейшую суперпозицию типа C^VD^V, эквивалентную заданному оператору F^V. Действительно, эквивалентность выражается уравнением F == С ´ D, а критерием простоты служит число столбцов в матрице С, равное числу строк матрицы D. На рис. 37 приведена иллюстрация этой интерпретации, соответствующая рассмотренному примеру (см. стр. 132).

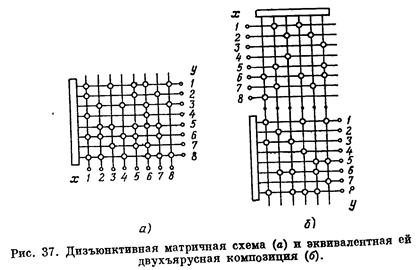
Там показаны некоторая дизъюнктивная матричная схема и эквивалентная ей последовательная двухъярусная композиция с минимальным промежуточным сечением.

12. Задача о кодировании

О перекодировании входных булевых векторов. Положим теперь, что в уравнении Y = ВvХ задана лишь матрица X, а матрицы Y и В требуется найти. Стремясь к содержательной постановке, уточним задачу: допустим, что все столбцы матрицы Х различны и требуется поставить в соответствие им также различные столбцы матрицы Y, причем число строк матрицы Y должно быть минимально.

В такой постановке задача интерпретируется как поиск элементарной матричной схемы, описываемой булевым матричным оператором B^V и осуществляющей такое пере-