Нахождение минимального дизъюнктивного базиса, страница 5

включается поэтому в решение. Легко находятся и определяющие элементы у²₂, y⁴₄ и y⁵₅, порождающие определяемые ими множества {y²₂},{y⁴₁}  и {y⁵₁,y⁵₅}, а также содержащие эти множества максимальные единичные миноры исходной булевой матрицы У:

Таким образом, в рассматриваемом примере правила редуцирования привели нас непосредственно к оптимальному решению, без построения матрицы L.

Весьма важно, что редуцирование путем нахождения определяющих элементов имеет в общем случае цепной характер, поскольку выбор очередного минора сопровождается сокращением числа единиц в текущем значении матрицы У*, а это может привести к появлению новых определяющих элементов.

Комбинирование методов. Описанные методы могут комбинироваться. Например, можно сначала редуцировать исходную матрицу Y, а затем построить матрицу L для оставшихся существенных элементов и искать ее кратчайшее строчное покрытие.

Пусть матрица, для которой надо найти кратчайшее минорное покрытие, имеет следующий вид:

Начнем с выделения в матрице У несущественных элементов. Для этого отыщем все пары строк и все пары столбцов, находящихся в отношении поглощения, и определим проекции поглощаемых рядов на поглощающие, как состоящие из несущественных элементов. Находим, что У₂ < У₆, У₃ < У₈, У₄ < У₁, Y₄< у₈, У₇ < Y₁, У³<У⁵, У³ < У⁶,У⁴ < У²,Y⁴<У⁶, У⁸ < У⁶ вследствие чего несущественными оказываются элементы y¹₆, y⁵₅, y⁷₆, y²₈, y⁴₈, y⁶₈ и т. д. Обозначая их символом «—», а оставшиеся единичные, т. е. существенные элементы — различными буквами (для удобства последующего изложения), приведем рассматриваемую матрицу Y к следующему редуцированному виду:

Анализируя полученную троичную матрицу (хотя существенные элементы и обозначены различными буквами, тем не менее они обладают одним значением 1, т. е. матрица остается троичной), в множестве существенных элементов можно выявить максимальные совместимые подмножества. Напомним, что в минорах, образованных строками и столбцами матрицы Y, в которых расположены элементы этих подмножеств, не должно находиться нулей, что следует из условия совместимости. Совокупность всех максимальных совместимых подмножеств из множества существенных элементов представим следующей булевой матрицей:

В этой матрице имеется несколько столбцов с одной единицей, что значительно облегчает решение задачи о кратчайшем строчном покрытии матрицы. Решение оказывается однозначным: оно образуется строками, отмеченными символом +.

Представим его следующей матрицей:

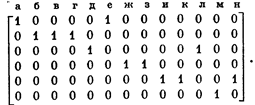Далее легко конструируется решение исходной задачи:

для каждого из подмножеств {а, е}, {б, в, г}, {д, л} и т. д. находится содержащий его, а в остальном произвольный, максимальный единичный минор матрицы У. Например, для подмножества {а, е} такой минор будет задаваться вектор-строкой

00000101, по которой легко восстанавливается соответствующий вектор-столбец.

Решение в целом будет представлено следующей парой матриц В и X, задающих соответственно строки и столбцы найденных миноров и удовлетворяющих уравнению Y = ВvХ: