 |
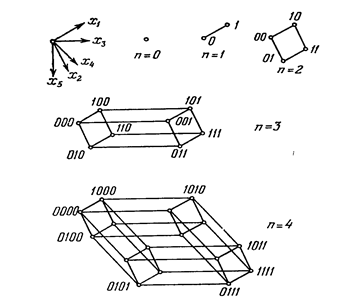
Рис 41. Построение четырехмерного куба
 |
соседние натуральные числа кодируются им соседними булевыми векторами.
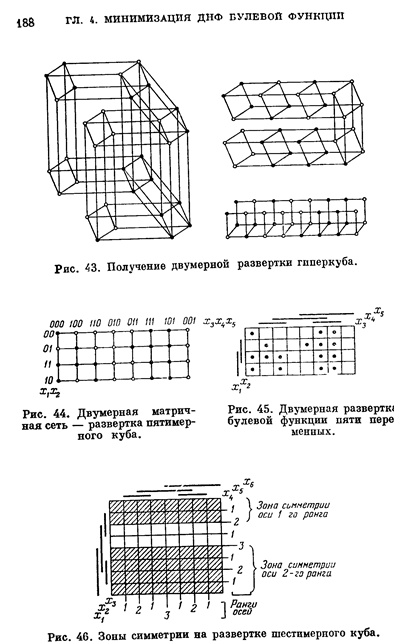
Модифицируя полученное изображение, перейдем к более удобной для последующего применения форме, показанной на рис. 45. Здесь узлы заменены клетками двумерной таблицы, а показанные сверху и слева и пронумерованные жирные линии (иногда прерывистые) соответствуют булевым переменным, образующим пространство М, и проведены против тех клеток, которые представляют наборы со значением 1 соответствующих компонент. В тех клетках, где булева функция принимает значение 1 (точнее говоря, она принимает значение 1 на элементах булева пространства, которым соответствуют эти клетки), находятся жирные точки.
Назовем эту заполненную точками форму двумерной разверткой булевой функции.
Одно из достоинств такой развертки заключается в том, что соседние элементы изображения всегда представляют соседние элементы изображаемого булева пространства, т. е. образуют двухэлементный интервал. Интервалом оказывается всегда и квадрат из четырех расположенных друг около друга элементов изображения.
В общем же случае соседние элементы булева пространства представляются элементами развертки, симметричными относительно некоторой ее оси и находящимися в зоне симметрии этой оси. При этом зона симметрии оси k-ro ранга образуется элементами, расположенными от оси не далее чем на расстоянии 2*. Как определяются ранги осёй, показано на рис. 46, где изображена двумерная разветка шестимерного куба. Там же приведены примеры зон симметрии.
На двумерной развертке легко выявляются интервалы булева пространства. При их распознавании полезно помнить, что любой элемент развертки n- мерного куба представляет собой интервал n-го ранта и что два интервала 1-го ранга, изображения которых на развертке симметричны относительно некоторой оси и полностью находятся в зоне ее симметрии, образуют интервал (i-1)-го ранга. Напомним, что интервал i-го ранга совпадает с характеристическим множеством соответствующей элементарной конъюнкции i-го ранга.
Визуальный метод минимзации булевых функций. Этот метод основан на визуальном распознавании интервалов булева пространства на его двумерной развертке и позволяет быстро находить оптимальные или близкие к ним интервальные покрытия характеристического множества М1 булевой функции с небольшим числом переменных, до шести, восьми или даже десяти. Последовательность выполняемых при этом операций может, в частности, повторять ту, которая дана в описании метода минимального соседства: нахождение в множестве М1 элементов с минимальным числом соседней и включение в решение покрывающих их интервалов.
 |
Данный метод характерен, в частности, тем, что выбор очередного, i-го шага связан с анализом частично покрытого множества М1, т. е. с рассмотрением некоторой «промежуточной» неполностью определенной булевой функции f, число неопределенных значений у которой растет с каждым шагом.
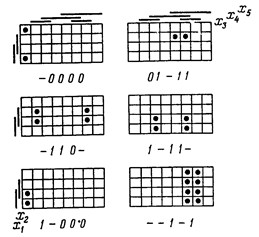
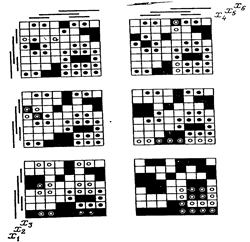
Очевидно, что метод применим и в тех ситуациях, когда неполностью определенной оказывается уже исходная функция f . Такая ситуация иллюстрируется рис. 48, где продемонстрированы шесть шагов процесса визуальной минимизации, на каждом из которых находится некоторый интервал (его элементы отмечены светлыми кружками), вносимый в решение. Элементы изображения, на которых булева функция, исходная или промежуточная, принимает неопределенное значение, зачернены.
 |
 |
47 48
Рис. 47. Разложение на интервалы изображения булевой функции, показанной на рис. 45.
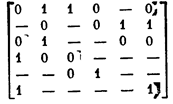 |
и остальные интервалы, образующие в совокупности решение, представляемое следующей матрицей:
17. Упрощение троичных матриц
Иногда булева функция f задается сразу в дизъюнктивной нормальной форме, представленной некоторой троичной матрицей U. Минимизировать ее в этом случае можно, воспользовавшись одним из описанных выше методов, но для этого потребуется перейти сначала к совершенной ДНФ, задав ее булевой матрицей В. Это не всегда практически просто, а иногда даже невозможно, если характеристическое множество минимизируемой функции f содержит слишком много элементов.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.