Коммутативность. Полиномы Жигалкина. Матричные преобразования в полином Жигалкина и обратно

P(позиционный ряд)            g(Код Грея)

0     0     0                              0     0     0

0     0     1                              0     0     1                             

0     1     0                              0     1     0

0     1     1                              0     1     1

1     0     0                              1     0     0

1     0     1                              1     0     1

1     1     0                              1     1     0

1     1     1                              1     1     1

                                   

 ;

g=dp;

1 0 1 1 0 0 1 0 0 1 1 0      p

1 1 1 0 1 0 1 1 0 1 0 1      g

Дифферинцирование булевых функций

1 0 0 1 1 0 0 1

1 1 0 0 0 1 1 1

0 1 0 1 1 1 1 0       - расстояние по Хэймингу

0 0 0 0 0 0 0 0

f(x),

· 

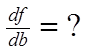
X	X	X	X	X
X	X	X	X	X
*	X	X	*	X			*
*	x	X	*	X			*

*	*	*	*	*	*
	*				*

Существует операция дифферинцирования по вектору

Если мы дифферинцируем функцию по какой-то переменной , то результат не будет зависеть от нее. Если дважды продифферинцировать по одной переменной, то результат будет равен нулю.

Если производная функции о некоторой переменной тождественно равна 0, то это значит, что функция не зависит от этой переменной.

1		1

Если четное количество единиц, то 0

Полиномы Жигалкина

Å нескольких элементарных конъюнкций называется полиномом.

Если в полиноме отсутствует отрицание, то такой полином называется полиномом Жигалкина.

Полином Жигалкина – каноническая форма представления булевых функций, представленных единственным образом.

2ⁿ – число различных конъюнкций

- число всех возможных

Векторное представление полиномов

Рассмотрим переход к полиному Жигалкина и обратно.

Полином Жигалкина {Ù,Å,1}

(если ab=0 или ортогональны, то aÚb=aÅb)

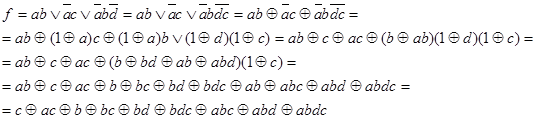
Рассмотрим обратное преобразование :

Обобщение полинома Жигалкина как полинома Рида-Маллера

Поляризованная переменная – для каждой переменной назначается условие, а совокупность переменных образует вектор.

a b c d e       Полином Рида-Маллера нулевой поляризации – полином Жигалкина.

1 0 0 1 1

Поиск оптимальной поляризации – сложная задача.

Матричные преобразования в полином Жигалкина и обратно

a b c          положительные конюнкции

0 0 0      |            1              |       

0 0 1      |            c              |        

0 1 0      |            b              |        

0 1 1      |            bc            |        

1 0 0      |            a              |          

1 0 1      |            ac            |         

1 1 0      |            ab            |         

1 1 1      |            abc          |         

C                       G                       D

Будем рассматривать отношения между этими конъюнкциями.

Построим матрицу :

	1	c	b	bc	a	ac	ab	abc
000	1	0	0	0	0	0	0	0
001	1	1	0	0	0	0	0	0
010	1	0	1	0	0	0	0	0
011	1	1	1	1	0	0	0	0
100	1	0	0	0	1	0	0	0
101	1	1	0	0	1	1	0	0
110	1	0	1	0	1	0	1	0
111	1	1	1	1	1	1	1	1

Элемент из G принимает единицу на элементе из С.

Рассмотрим операцию Кронекеровского произведения матриц : AÄB=C

[C]=[A]´[B]

| 1  0 |³

R=  | 1  1 |

Все строки R представляют Кронекерское произведение первой строки. Производная от предыдущей строки :

Элемент a^к_i, где к – строка, равен сумме a_i^k-1Åa_i-1^k-1, где i -  столбец.