Строка и, безызбыточной матрицы U обязательна в том" и только том случае, когда не будет вырожденным минор, образуемый пересечением строк, неортогональных или смежных со строкой и,, со столбцами, в которых строка и, имеет значение «—».
Действительно, если этот минор вырожден, то для любого элемента а интервала и; в матрице U найдется такой интервалuj, который содержит элемент а (если Ui и uj неортогональны) или некоторого его соседа (если Ui, и Uj смежны). Это означает, что элемент а принадлежит по крайней мере двум максимальным интервалам — в первом случае оба они представлены в матрице U, во втором случае один из них может быть получен обобщенным склеиванием интервалов и; и uj.
Если же минор не вырожден, то найдется ортогональный ему булев вектор. Присвоив значения его компонент соответствующим компонентам строки и,, мы получим элемент интервала и,, не имеющий в множестве М1 соседей за. пределами этого интервала, что и доказывает обязательность строки и,.
Рассмотрим следующую безызбыточную матрицу:
 |
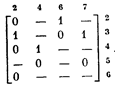 |
Он оказывается невырожденным, следовательно, строка 1 обязательна. В этом легко убедиться, построив ортогональный минору булев вектор 1111 и заменив значениями его компонент значения «—» соответствующих компонент строки 1. Полученный при этом булев вектор 1101011 будет представлять собой именно такой элемент характеристического множества М1, который принадлежит только рассматриваемому максимальному интервалу и не имеет в множестве М соседей за пределами интервала.
Анализируя аналогично следующие строки матрицы U, мы придем к выводу, что все они обязательны, кроме последней, которой соответствует вырожденный минор. Но просто так выбросить строку 6 из матрицы U нельзя — матрица безызбыточна. Необязательность строки 6 означает лишь, что ее можно заменить какой-то другой строкой, в данном случае не присутствующей в матрице U. Однако такая операция не приведет к уменьшению числа строк в матрице. Следовательно, можно считать доказанным, что рассматриваемая матрица U представляет кратчайшую ДНФ.
Построение допустимых совокупностей максимальных интервалов. Вернемся теперь к ситуации, в которой матрица U представляет множество А всех максимальных интервалов характеристического множества М1, и рассмотрим задача выбора из нее такой допустимой совокупности максимальных интервалов, для которой, согласно определению, найдется содержащее ее кратчайшее интервальное покрытие множества М1.
Представим себе этот выбор как многошаговый процесс, при котором текущая ситуация характеризуется разбиением множества А на три части: некоторую уже построенную допустимую совокупность А+, такое множество А-, относительно которого известно, что существует некоторое кратчайшее интервальное покрытие множества М1, содержащее А+ и не пересекающееся с А-, и текущий остаток А*, определяемый как А \ (А+ U A-). Все три множества являются переменными, причем в качестве исходного значения множества А* может быть принято ядро решения, состоящее из обязательных интервалов, а в качестве исходного значения множества А- — антиядро.
Очередной шаг состоит в добавлении в множество А- некоторого элемента, выбираемого из множества А*, причем такого, чтобы новое значение множества А- также обладало описанным выше качеством. Эта операция сопровождается, если это возможно, расширением множества А+, а также соответствующим сокращением множества А*.
Процесс продолжается до некоторой тупиковой ситуации, когда в множестве А* уже не удается найти элементов с требуемыми свойствами. Тогда возникает необходимость в организации просмотра различных вариантов продолжения построения интервального покрытия множества М1 или в выборе какого-либо конкретного варианта, перспективного, но не гарантирующего оптимальность получаемого при его реализации результата.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.