В тех случаях, когда описанный способ упрощения ДНФ оказывается трудоемким, можно рекомендовать попытаться упростить сначала ДНФ более быстродействующим способом, а затем уже устранять избыточность из полученного результата.
Например, довольно эффективной оказывается следующая процедура: в матрице U отыскиваются пары смежных строк и к ним применяется операция обобщенного склеивания. Если продукт поглощает некоторую из этих строк (или обе), то он ее заменяет, в противном случае не используется.
Нетрудно проверить, что в применении к рассмотренному примеру этот метод приведет к тому же результату.
Нахождение обязательных строк. Во многих практических ситуациях задача построения кратчайшей ДНФ, исходя из сокращенной ДНФ, может быть редуцирована путем нахождения в последней обязательных членов, которые должны присутствовать в любой кратчайшей ДНФ с безызбыточными членами и даже в любой безызбыточной ДНФ. В троичной матрице U, задающей сокращенную ДНФ, в этом случае отыскиваются соответствующие обязательные строки.
Очевидно, что строка и; матрицы U является обязательной, т. е. должна быть непременно включена в решение, если ее нельзя выбросить с самого начала. Следовательно, она обязательна, если минор, образуемый пересечением других строк, неортогональных строке и;, со столбцами, где она имеет значение «—», не вырожден. Совокупность обязательных строк составляет ядро решения.
С другой стороны, строка, покрываемая ядром, не сможет принадлежать ни одному из минимальных покрытий и даже ни одному из безызбыточных. Такая строка удовлетворяет условию: минор, образованный пересечением строк, принадлежащих ядру и неортогональных данной строке, со столбцами, в которых она имеет значение «—», вырожден. Совокупность таких строк назовем антиядром решения. Очевидно, что эти строки можно сразу исключить из дальнейшего рассмотрения, удалив их из матрицы U.
В результате нахождения ядра и антиядра решения производимый при поиске оптимального покрытия перебор может значительно сократиться.
Например, пусть множество А всех простых импликант булевой функции f задано троичной матрицей
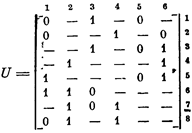 |
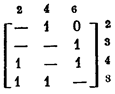 |
Начнем с поиска обязательных строк. Соответствующий строке 1 минор не вырожден, следовательно, эта строка обязательна. Подобным образом находим, что обязательны также строки 2, 4, 5 и 6,8 Остальные строки проверяются на принадлежность антиядру. Например, образуя соответствующий строке 3 минор из неортогональных ей строк ядра
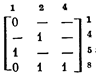 |
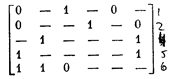 |
содержащий лишь обязательные строки. Очевидно поэтому, что он представляет оптимальное решение.
Допустим теперь, что исходная троичная матрица U задает не сокращенную, а некоторую бозызбыточную ДНФ булевой функции f . Спрашивается, можно лн и в этом случае выявить ядро решения непосредственно в матрице U, не прибегая к предварительному получению множества всех простых импликапт путем соответствующего расширения матрицы U?
Оказывается, что можно. Прежде всего, заметим, что поскольку обязательные строки должны содержаться в любой безызбыточной ДНФ, то все они, очевидно, содержатся и в данной матрице U. Остается распознать их там.
Ранее было показано, что максимальный интервал Uj множества М1 обязателен, если он обладает некоторым элементом, не имеющим в множестве М1 таких соседей, которые не принадлежали бы этому интервалу. Очевидно, что такие соседние элементы могли бы находиться только в таких максимальных интервалах, которые неортогональны интервалу и, или смежны с ним.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.