![]() (*)
(*)
– однородную систему линейных уравнений с ![]() неизвестными
неизвестными
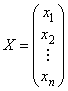 ,
, 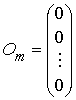 – нулевой столбец высоты m.
– нулевой столбец высоты m.
В соответствии с теоремой 3.4 ![]() – ранг отображения. Пусть
размерность ядра равна
– ранг отображения. Пусть
размерность ядра равна ![]() . Из свойств
множества решений однородной системы уравнений вытекает, что
. Из свойств
множества решений однородной системы уравнений вытекает, что ![]() (доказать самостоятельно,
что множество решений системы (*) – линейное подпространство размерности
(доказать самостоятельно,
что множество решений системы (*) – линейное подпространство размерности ![]() ).
).
Общее решение системы (*) было представлено в виде (см. линейная алгебра)
![]() , где
, где ![]() – фундаментальная система
решений, следовательно
– фундаментальная система
решений, следовательно ![]() ,
, ![]() – линейная комбинация
векторов
– линейная комбинация
векторов ![]() , т.е.
, т.е.
![]() , координатные столбцы которых
, координатные столбцы которых ![]() –
линейно независимы, следовательно, эти векторы тоже линейно независимы и значит
–
линейно независимы, следовательно, эти векторы тоже линейно независимы и значит
![]() – базис в
– базис в ![]() , т.е.
, т.е. ![]() .
.
Таким образом, ![]() .
.
3.3. Изменение матрицы линейного отображения
при замене базисов
Рассмотрим
линейный оператор ![]() , если в
пространствах
, если в
пространствах ![]() и
и ![]() выбраны базисы
выбраны базисы ![]() ,
, ![]() соответственно, то
соответственно, то ![]() определяется матрицей
определяется матрицей ![]() . Пусть
. Пусть ![]() и
и ![]() - другая пара базисов в
- другая пара базисов в ![]() и
и ![]() соответственно,
соответственно, ![]() связаны с
связаны с ![]() матрицами переходов Т и
Р, т.е. (см. раздел 1)
матрицами переходов Т и
Р, т.е. (см. раздел 1)
![]()
В базисах ![]() оператор
оператор ![]() имеет матрицу
имеет матрицу ![]() . Как связаны
матрицы
. Как связаны
матрицы ![]() и
и ![]() ?
?
Пусть:
![]() –
образ вектора
–
образ вектора ![]() при
отображении
при
отображении ![]() ;
;
Х, Х' – координатные столбцы вектора ![]() в
базисах е, е';
в
базисах е, е';
![]() –
координатные столбцы вектора
–
координатные столбцы вектора ![]() в
базисах
в
базисах ![]() . Из раздела 1
известно, что
. Из раздела 1
известно, что
![]() .
.
Подставим X, Y в формулу (3.4) и получим:
![]() .
.
Так как матрица
перехода всегда является невырожденной, то ![]() .
Умножим последнее равенство на матрицу
.
Умножим последнее равенство на матрицу ![]() слева, получим
слева, получим
![]() , но
, но ![]() , откуда получаем
, откуда получаем
![]() (3.5)
(3.5)
- формулу преобразования матрицы линейного оператора при замене базисов.
Из определения отображения
![]() :
: ![]() (
(![]() – существует единственный)такой, что
– существует единственный)такой, что ![]() ; если
справедливо и обратное, т.е. каждый
; если
справедливо и обратное, т.е. каждый ![]() является
образом только одного вектора
является
образом только одного вектора ![]() ,
то отображение
,
то отображение ![]() называется
взаимно однозначным.
называется
взаимно однозначным.
Иначе, если
![]() , то
, то ![]() , или
, или
![]() такой, что
такой, что ![]() .
.
Теорема 3.6. Отображение ![]() –
взаимно однозначно (биективно) тогда и только тогда, когда размерности
пространств совпадают и равны рангу отображения
–
взаимно однозначно (биективно) тогда и только тогда, когда размерности
пространств совпадают и равны рангу отображения ![]() .
.
Доказательство. В этом случае отображение ![]() является
и наложением, т.е. rang
является
и наложением, т.е. rang![]() = т,
и вложением, т.е.
= т,
и вложением, т.е. ![]() (на основании
теоремы 3.5).
(на основании
теоремы 3.5).
Определение. Взаимно однозначное отображение называется изоморфизмом.
Если существует изоморфизм ![]() на
на ![]() , то
, то ![]() и
и ![]() называются изоморфными.
называются изоморфными.
Теорема 3.7. Два пространства изоморфны тогда и только тогда, когда их размерности равны. Доказательство (см. теорему 3.3 и теорему 3.5).
Значение теоремы об изоморфизме состоит в том, что линейные пространства могут состоять из чего угодно: столбцов, многочленов, чисел, функций, матриц, направленных отрезков, дынь, арбузов – природа их элементов роли не играет, когда изучаются только свойства, связанные с операциями сложения и умножения на число. Все эти свойства у двух изоморфных пространств совершенно одинаковы. С алгебраической точки зрения два изоморфных пространства тождественны. Если условимся не различать эти пространства, то в силу теоремы 3.3 для каждой размерности найдется только одно линейное пространство.
Пример 3.1. Определить ранг и дефект линейного преобразования,
а также найти базисы образа и ядра ![]() при преобразовании
при преобразовании ![]() .
.
![]() .
.
Решение. Пусть в ![]() выбран базис
выбран базис ![]() , тогда в этом базисе матрица
преобразования
, тогда в этом базисе матрица
преобразования ![]() будет иметь
вид:
будет иметь
вид:
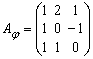 .
.
По определению вектор ![]() принадлежит образу
принадлежит образу ![]() при преобразовании
при преобразовании ![]() в том и только том
случае, когда найдется вектор
в том и только том
случае, когда найдется вектор ![]() такой,
что
такой,
что ![]() , или в координатной
записи по формуле (3.4):
, или в координатной
записи по формуле (3.4):
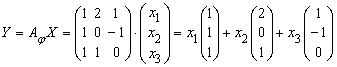 .
.
Это равенство означает, что образ ![]() совпадает с линейной оболочкой системы векторов
совпадает с линейной оболочкой системы векторов ![]() , так как
, так как ![]() . Следовательно,
ранг оператора
. Следовательно,
ранг оператора ![]() , который
совпадает с рангом его матрицы, равен двум. В качестве базиса можно взять любой
базис линейной оболочки векторов
, который
совпадает с рангом его матрицы, равен двум. В качестве базиса можно взять любой
базис линейной оболочки векторов ![]() , например,
, например,
![]() – они линейно независимы.
– они линейно независимы.
Аналогично вектор ![]() принадлежит
ядру тогда и только тогда, когда
принадлежит
ядру тогда и только тогда, когда ![]() , или,
в координатной записи:
, или,
в координатной записи:
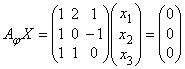 .
.
Это однородная система линейных уравнений, ранг которой равен двум, значит, она эквивалентна следующей системе:
![]() , полагая в которой, например,
, полагая в которой, например, ![]() ,
получаем
,
получаем ![]() , т.е. базис ядра
состоит из одного вектора
, т.е. базис ядра
состоит из одного вектора ![]() .
.
При этом по теореме 3.5, размерность ядра равна:
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.