Линейные преобразования и квадратичные формы: Учебное пособие, страница 6

В частности, множество образов всевозможных векторов из пространства  является подпространством в пространстве . Будем обозначать это подпространство , которое называется множеством значений отображения , или образом пространства при отображении .

Определение. Размерность образа пространства  при отображении  называетсярангом этого отображения.

Обозначения: .

Если , т.е. , то каждый вектор из является образом некоторого вектора из пространства . Отображение, обладающее этим свойством, называется сюръективным или наложением (говорят  – отображение на).

Теорема 3.2. Множество всех векторов из , переходящих при отображении  в нулевой вектор, является подпространством в .

Доказательство. Если , , то по определению линейного отображения можем записать:

1) ;

2) .

Эти равенства означают, что множество всех векторов из , переходящих при отображении  в нулевой вектор, является подпространством в .

Определение. Подпространство векторов из пространства , отображающихся в нулевой вектор, называется ядром отображения  и обозначается .

Таким образом,  .

Ядро линейного отображения не может быть пустым, так как содержит, по крайней мере, один вектор – нулевой.

Действительно,  т.е. при линейном отображении нулевой вектор  переходит в нулевой вектор .

Определение. Размерность ядра называется дефектом линейного отображения.

Определение. Отображение, при котором разные векторы имеют разные образы, называется инъективным или вложением.

Теорема 3.3. Отображение  является инъективным тогда и только тогда, когда его ядро есть нулевое подпространство

.

Доказательство. () Пусть  – инъективно и , тогда в пространстве  существуют векторы, имеющие не один прообраз, а, по крайней мере, два, таким является, например, нулевой вектор  (смотри определение и утверждение 3.2). Но это противоречит условию теоремы.

() Пусть и отображение не инъективно. Это значит, что существует вектор , который имеет два разных прообраза, т.е. существуют векторы такие, что  и . В этом случае ядро содержит, по крайней мере, один ненулевой вектор  (ядро - ненулевое подпространство), так как

, следовательно,, что, опять таки, противоречит условию теоремы. Следовательно,  – инъективно.

3.2. Координатное представление линейных отображений

Пусть  – базис в , тогда образ произвольного вектора из пространства :  можно представить в виде

                               (3.2)

Пусть  – базис , тогда каждый из векторов  можно разложить по базису  f

Если  ,  то (3.2) можно переписать в виде (подставить  в  (3.2)):

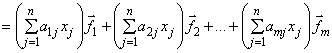, следовательно,

                   (3.3)

Коэффициенты  – координаты векторов  в базисе  f  образуют матрицу , размеров

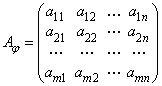, которая называется матрицей линейного отображения  в паре базисов  е  и  f.

Матрица  составлена из координатных столбцов образов базисных векторов  в базисе  f .

Если 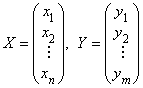 – координатные столбцы векторов  и  соответственно, то равенство (3.3) в матричной форме принимает вид

                                                           (3.4)

При выбранных базисах е и  f  в пространствах  и  соответственно, каждая матрица размеров служит матрицей некоторого линейного отображения , т.е. выбор базисов устанавливает взаимно однозначное соответствие между линейными отображениями  и матрицами размеров.

Теорема 3.4. Ранг матрицы линейного отображения равен рангу этого отображения .

Доказательство. Пусть  и  – номера столбов матрицы , в которых расположен базисный минор. Это значит, что векторы   линейно независимы и, следовательно, каждый вектор  () есть их линейная комбинация (см. теорему о базисном миноре).

Следовательно, образ любого вектора  можно выразить только через векторы , т.е. эти векторы образуют базис в  – множестве значений отображения , но их число равно размерности , т.е. рангу отображения, следовательно, .

Теорема 3.5. Сумма ранга () и дефекта отображения (размерности его ядра) равна размерности отображаемого пространства

.

Доказательство. Пусть , , тогда по определению ядра линейного отображения  и формуле (3.4) получаем