Линейные преобразования и квадратичные формы: Учебное пособие, страница 5

Доказательство. Если

,

.

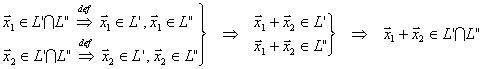Теорема 2.5.  .

Доказательство.  Рассмотрим в сумме  следующую систему векторов:

а) если  – ненулевое подпространство, то возьмём базис  в  и дополним его до базиса в  векторами  и векторами  до базиса в ;

б) если  – нулевое подпространство, то просто возьмём объединение базисов  и  в  и в  соответственно.

Покажем, что любой вектор  является линейной комбинацией построенной системы векторов. Это следует из определения

  , где , , следовательно, , , следовательно, – линейная комбинация построенной системы векторов.

Теперь покажем, что эта система векторов линейно независима.

Возьмём какую-либо линейную комбинацию этих векторов и приравняем к нулевому вектору

 .                                        (*)

Вектор , а из (*) следует  (так как ,  – базис в ), следовательно, , но тогда по теореме 2.3 заключаем, что .

Аналогично, вектор , а из (*) следует, что

(так как ,  (; ) – базис в ), тогда по теореме 2.3 заключаем, что .

Таким образом, равенство (*) принимает вид

, но тогда и , так как  – базис в .

В результате заключаем, что равенство (*) возможно лишь для тривиальной линейной комбинации, следовательно, система векторов

– линейно независима и по определению образует базис в .

Теперь по построению

,  ,  , следовательно,      .

Следствие 2.1. Если dimL' + dimL" > п, то , так как L' + L" – подпространство в  и поэтому (теорема 2.1) .

Если , то L' + L"называется прямой суммой подпространств и обозначается

Следствие 2.2. .

Теорема 2.6.    такие, что .

Доказательство. Пусть таких разложения два, т.е.  и , где , , тогда , следовательно, . Очевидно, что вектор , но , значит , т.е. . Аналогично .

Пример 2.1. Найти размерность и базис линейного подпространства, являющегося линейной оболочкой векторов:

,  .

Решение. Составим из координатных столбцов векторов системы матрицу и с помощью элементарных преобразований определим ее ранг. Ранг этой матрицы будет совпадать с числом линейно независимых векторов в системе и значит, будет равен размерности оболочки векторов (см. раздел 1). Матрица из координатных столбцов имеет вид:

.

Умножим элементы первого столбца на –2 и прибавим к соответствующим элементам второго и пятого столбцов, затем элементы первого столбца умножим на –1 и прибавим к соответствующим элементам третьего и четвертого столбцов. В результате получим матрицу эквивалентную исходной, которая будет иметь вид:

 .

Вычитая теперь из третьего столбца второй, а из пятого – четвертый, получаем опять матрицу, которая эквивалентна исходной:

.

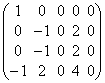Таким образом, ранг этой матрицы равен трем и размерность линейной оболочки тоже будет равна трем. В качестве базиса можно взять векторы  (вектор  является линейной комбинацией векторов  и поэтому не может быть базисным).

3. ЛИНЕЙНЫЕ ОТОБРАЖЕНИЯ (ОПЕРАТОРЫ)

3.1. Определение линейного отображения

Рассмотрим два линейных пространства  размерностей п и т соответственно.

Определение. Отображением  пространства  в пространство  называется закон, по которому каждому вектору  ставится в соответствие единственный вектор .

Обозначения: , или .

Вектор  называется образом вектора , а вектор – прообразом вектора  при отображении .

В дальнейшем рассматриваются лишь линейные отображения.

Определение. Отображение  называется линейным, если   выполняются равенства:

1)  ;

2)  .

Из этого определения сразу следует, что линейная комбинация векторов при линейном отображении  переходит в линейную комбинацию образов с теми же коэффициентами, т.е. справедлива формула

           (3.1)

(получить самостоятельно из свойств 1), 2) определения).

Если пространства  и  совпадают, т.е. т = п, то отображение называется преобразованием пространства.

Теорема 3.1. При линейном отображении  линейное подпространство  переходит в линейное подпространство , причем размерность L" не превосходит размерности , т.е. .

Доказательство. Пусть  – базис в L', тогда  имеем

следовательно, произвольный элемент множества – образов всех векторов из L'есть линейная комбинация векторов , т.е. – линейная оболочка этих векторов и значит, является линейным подпространством из пространства  (теорема 2.1). Размерность линейной оболочки, очевидно, не превосходит числа векторов этой оболочки (теорема 2.2), т.е..