Линейные преобразования и квадратичные формы: Учебное пособие, страница 3

2) любой вектор из L является линейной комбинацией векторов этой системы.

Пусть базис пространства состоит из пвекторов , тогда по определению :

.                                   (1.1)

Коэффициенты этой линейной комбинации  называются координатами вектора  в базисе , равенство (1.1) называется разложением вектора  по базису . Очень часто, для сокращения записи и удобства, вектор обозначается перечислением координат:

,                                                 (1.2) считается, что записи (1.1) и (1.2) эквивалентны.

Обозначим  – матрицу-строку из базисных векторов, 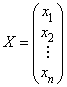 – координатный столбец вектора , тогда по определению произведения матриц

.                                                  (1.3)

Теорема 1.4. Если в пространстве L задан базис е, то координаты любого вектора в этом базисе определяются однозначно.

Доказательство. Предположим, что и , тогда вычитая из первого равенства второе, получим . Так как система векторов  линейно независима (см. определение базиса), то все коэффициенты полученной линейной комбинации равны нулю (она тривиальная!), следовательно , т.е.  (k = ).

Теорема 1.5. Координаты вектора  равны сумме координат векторов  и .

Координаты вектора  равны координатам вектора  умноженным на .

Доказательство. Пусть ебазис вL, тогда по формуле (1.3) , . Пусть , тогда

 , следовательно, по теореме 1.5

 (k = ).

Аналогично, если , то  и по теореме 1.4

   (k = ).

Теорема 1.6. Если в линейном пространстве существует базис из n векторов, то любой другой базис состоит из того же числа векторов.

Доказательство. Пусть  и  два базиса в , причём . Разложим каждый из векторов  по базису e и составим матрицу, столбцами которой будут координатные столбцы векторов . Эта матрица имеет ранг n (так как e базис и координатные столбцы линейно независимы), следовательно, по теореме о базисном миноре столбцы матрицы линейно зависимы ( последних столбцов являются линейными комбинациями первых n столбцов), таким образом  – линейно зависимы и не могут быть базисом в .

Определение. Линейное пространство, в котором существует базис из n векторов, называется п-мерным и обозначается , число п называется размерностью пространства и обозначаетсяdimL (dimension – размерность).

Может случиться так, что  в L найдется плинейно независимых векторов, такое пространство называется бесконечномерным.

Теорема 1.7. В  каждая линейно независимая система из пвекторов является базисом.

Доказательство. Любой вектор из пространства  представляется в виде линейной комбинации векторов этой системы, если это не так, то по теореме 1.1 существует линейно независимая система из n + 1 векторов, что противоречит определению базиса.

Теорема 1.8. В линейном пространстве  каждую линейно независимую систему из т < п векторов можно дополнить до базиса в .

Доказательство. Пусть дана линейно независимая система  из т векторов. К этим т векторам можно добавить еще один вектор, линейно независимый с ними, иначе  - базис в, чего по теореме 1.5 не может быть. Рассуждая аналогично при т + 1, т + 2, ..., п – 1, получим систему из n линейно независимых векторов, которая по теореме 1.7 будет базисом в .

1.3. Замена базиса линейного пространства

Пусть в  даны два базиса:  и , тогда каждый вектор из базиса  f  можно разложить по базису е, т.е.

     (j = )                         (1.4)

из координатных столбцов векторов  в базисе е можно составить квадратную матрицу порядка п

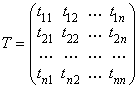, которая называется матрицей перехода от базиса е к базису  f. Эта матрица всегда является невырожденной, так как e и  f  - базисы линейного пространства, и, если detT = 0, то один из столбцов матрицы T есть линейная комбинация других столбцов этой матрицы, т.е. по крайней мере один из векторов  является линейной комбинацией других векторов из  f , что противоречит определению базиса.

Равенства (1.4) в матричной форме можно записать в виде f = eТ, умножая это равенство на  справа, получаем

   или   , т.е.  – матрица перехода от базиса  f  к базису е.

Выясним, как связаны координаты одного и того же вектора  в базисах  е  и  f.

Пусть ,  – координатные столбцы вектора  в базисах е и  f  соответственно, тогда     и   f = eT,  таким образом