Санкт-Петербургский Государственный Технический Университет
Факультет Технической Кибернетики
Кафедра Системного Анализа и Управления
![]() Курсовая работа
Курсовая работа
Вычислительная математика
Изучение математического пакета MatLab.
Решение задачи интерполирования.
выполнил: студент Четаев А. Ю.
гр. 2082/1
проверил: Кирсяев А. Н.
Санкт-Петербург
2006 г.
Оглавление 2
Постановка задачи 3
Теоретическая часть 3
Описание программы 4
Блок-схемы функций 5
sfunc(x) 5
lagranzh(t,x) 5
tchebishev(c,d,n) 8
Листинг 8
Kursovaja.m.. 8
sfunc.m.. 9
lagranzh.m.. 10
w.m.. 10
ravnomer.m.. 10
tchebishev.m.. 10
Расчеты 11
Выводы 12
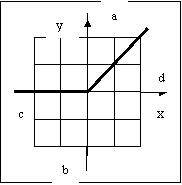 Сравнить графики заданной функции f(x) и интерполяционных полиномов Pn(x) для n=2, 6, 14 на интервале x=[c,d] при
двух вариантах выбора узлов:
Сравнить графики заданной функции f(x) и интерполяционных полиномов Pn(x) для n=2, 6, 14 на интервале x=[c,d] при
двух вариантах выбора узлов:
Использовать формулу Лагранжа для построения интерполяционного полинома.
a = d = 1;
b = c = -1;
Задача интерполирования заключается в построении полинома, совпадающего с заданной функцией в заданных точках, называемых узлами.
В данной работе используется интерполяционный полином
Лагранжа, определяется формулой:![]() , где
, где ![]() - узел,
- узел, ![]() -
исследуемая функции, а
-
исследуемая функции, а 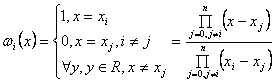 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.