Санкт-Петербургский Государственный Политехнический Университет
Факультет Технической Кибернетики
Кафедра Системного Анализа и Управления
Работа №1
Курс: «Вычислительная математика»
Тема: «Интерполирование функции»
Выполнил: ст. гр. 2082/1
Хатько И.О.
Проверил:
Санкт-Петербург
2006
Постановка задачи
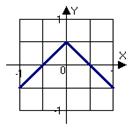
При помощи математической системы MatLab требуется смоделировать графики заданной функции, приближая функцию степенным полиномом степеней n = 2, 6, 14, на интервале [-1, 1] , используя при этом два способа выбора узлов:
равномерно с шагом h = 2/n;
по Чебышеву.
Для построения степенного полинома должен использоваться метод Ньютона.
По результатам моделирования должны быть построены следующие графики:
функции;
зависимости погрешности приближения функции степенным полиномом от способа выбора узлов для каждого значения степени полинома;
зависимости погрешности приближения функции степенным полиномом от величины степени полинома для каждого способа выбора узлов.
Данные графики необходимо проанализировать, сравнить между собой и сделать соответствующие выводы.
В приложении содержаться графики погрешностей для всех методов.
Методы решения и формулы
Для моделирования графика кусочно-линейной функции используется метод интерполирования сплайнами. Каноническая форма такого сплайна имеет вид
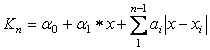 ,
,
где суммирование ведется по узлам сплайна, а n, соответственно, - порядок сплайна. Функция задается ее узловыми и крайними точками, которые и используются для решения задачи кусочно-линейного интерполирования. Для этого составляется система из n+1 уравнения и находятся параметры αо, α1, ai.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.