Интерполирование функции при помощи математической системы MatLab, страница 5

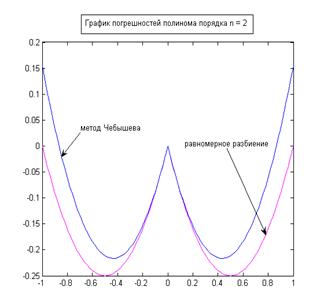
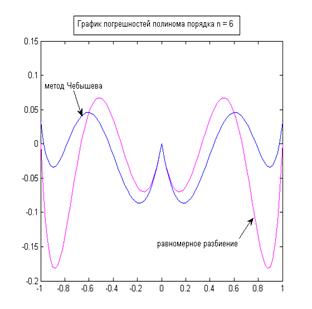
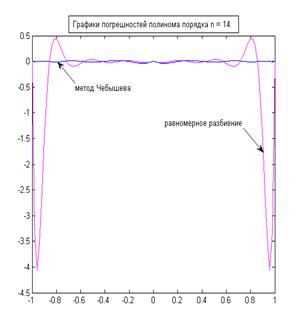
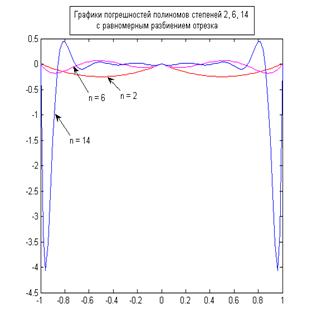
Для равномерного разбиения на краях отрезка наблюдаются значительные отклонения графика полинома от графика функции. При этом, как следует из теории (феном Рунге) при увеличении степени полинома (а значит и числа узлов) для многих функций осцилляция на краях области определения функции, обусловленная равномерным выбором узлов интерполяции, будет возрастать. Что, в сущности, мы и наблюдаем на графиках.

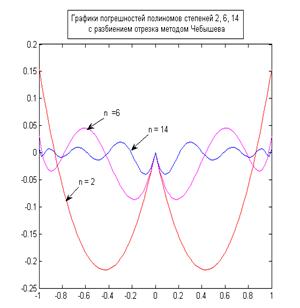
Сравнение графиков погрешностей для разбиения Чебышева и равномерного разбиения говорит о том, что использование метода Чебышева позволяет снизить осцилляцию на краях области определения, и следовательно значительно понизить погрешность построения полинома. Как известно из теории, метод Чебышева нацелен на минимизацию максимального отклонения полинома от функции. Это подтверждается графически. Из графиков также видно, что погрешность построения полинома при выборе узлов методом Чебышева уменьшается при повышении порядка интерполирования, хотя и не сводится к нулю.

Таким образом, из двух представленных методов выбора узлов наиболее точным является метод Чебышева, точность которого увеличивается с повышением порядка интерполирования.

Приложение.