Интерполирование функции при помощи математической системы MatLab, страница 2

В соответствии с постановкой задачи узлы интерполирования функции полиномом Ньютона выбираются двумя способами. В первом случае выбор ведется равномерно с шагом h = 2/n, и каждый узел вычисляется по формуле x_i = -1 + hi,  i = 0,…,n. Во втором случае для выбора узлов используется метод Чебышева, и узлы вычисляются по формуле 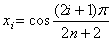,  i = 0,…,n.

Интерполяционный полином Ньютона строится на основе уравнений связи между значениями функции и построенными соответствующими разделенными разностями:

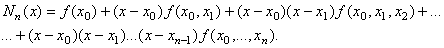
Вычисление разделенных разностей выполняется табличным методом по формуле

.

Таким образом получается таблица (реализуемая как матрица) размера (n+1)x(n+1). Для построения полинома Ньютона используется первая строка полученной матрицы.

Структура данных и программы

Программа состоит из следующих модулей:

1. Splin.dat – Файл данных, содержащий крайние и узловые точки заданной кусочно-линейной функции. Первая строка представляет собой набор аргументов, а вторая – соответствующий набор значений функции.
2. Hx.m – Функция равномерного разбиения отрезка Hx(a,b,n), принимающая на входе концы отрезка a и b и порядок интерполирования n, и дающая на выходе вектор узлов интерполирования, состоящий из n+1 точки.
3. Chx.m – Функция разбиения отрезка [-1, 1] по Чебышеву Chx(n), принимающая на входе порядок интерполирования n и дающая на выходе вектор узлов интерполирования, состоящий из n+1 точки.
4. Pspline.m – Функция интерполирования сплайна Pspline(Sp,t), принимающая на входе матрицу точек Sp кусочно-линейной функции, загружаемую предварительно из файла данных Splin.dat, и набор узлов t, полученных при помощи функции Hx или Chx. На выходе мы получаем вектор значений функции в данных узлах.
5. RRasn.m – Функция вычисления разделенных разностей RRasn(n,f,x), принимающая на входе порядок интерполирования n, вектор f значений функции в узлах, полученный при помощи функции Pspline, и вектор узлов x, полученный при помощи функции Hx или Chx. На выходе мы получаем матрицу разделенных разностей размера (n+1)x(n+1).
6. Newton.m – Функция построения полинома Ньютона Newton(n,f,t,x), принимающая на входе порядок интерполирования n, вектор f значений функции в узлах, полученный при помощи функции Pspline, вектор узлов t, полученный при помощи функции Hx или Chx, и узел x. Вычисление разделенных разностей ведется при помощи функции RRasn. На выходе мы получаем значение полинома Ньютона в заданном узле x.
7. GrSp.m – Скрипт построения графика заданной кусочно-линейной функции, использующий файл данных Splin.dat и функцию Pspline.
8. GrPogr.m – Функция GrPogr(n) построения графиков погрешностей интерполирования двух способов выбора узлов для заданного порядка интерполирования n.
9. GrPogrR.m – Скрипт построения графиков погрешностей интерполирования трех различных порядков. Графики строятся в отдельном окне для каждого из двух способов выбора узлов.
10. main.m – Скрипт основной программы, строящей по очереди графики функции и погрешностей при помощи скриптов GrSp, GrPogrR и функции GrPogr.