Изучение математического пакета MatLab, решение задачи интерполирования, страница 6

%x - массив абсцисс точек

function y=sfunc(x)

for i = 1:length(x)

  if (x(i) < 0) y(i)=0;

  else y(i) = x(i);

  end

end

lagranzh.m

function z=lagranzh(t,x)

for j = 1:length(t)

    z(j)=0;

    for i = 1:length(x)

         z(j)=z(j)+sfunc(x(i))*w(t(j),x,i)/w(x(i),x,i);

    end

end

w.m

function z=w(t,x,j)

for k = 1:length(t)

    z(k)=1;

    for i = 1:length(x)

        if (i ~= j) z(k)=z(k)*(t(k)-x(i));

        end

    end

end

end

ravnomer.m

function z=ravnomer(c,d,n)

if (c<=d) & (n>=2)

    for i= 0:n

        z(i+1)=c+(d-c)*i/n;

    end

else z=0;

end

tchebishev.m

function z=tcebishev(c,d,n)

if (c<d) & (n>=2)

    for i = 0:n

        z(i+1) = 0.5*((d-c)*cos((2*i+1)/(2*n+2)*pi)+c+d);

    end

else

    z=0;

end

Расчеты

1.  Интерполяционные полиномы 2 порядка и погрешности вычислений.

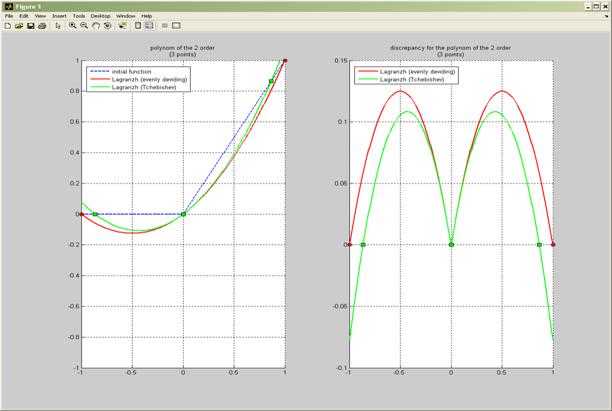
2.  Интерполяционные полиномы 6 порядка и погрешности вычислений.

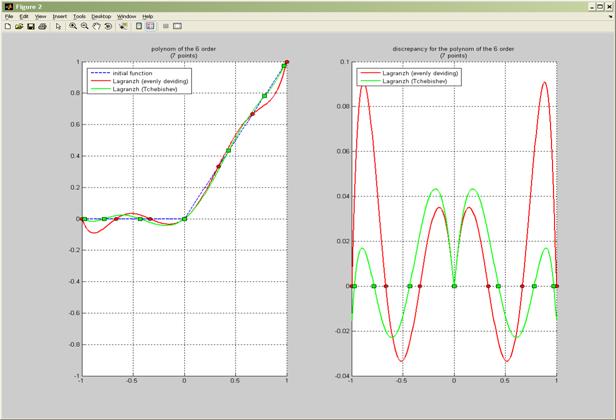
3.  Интерполяционные полиномы 14 порядка и погрешности вычислений.

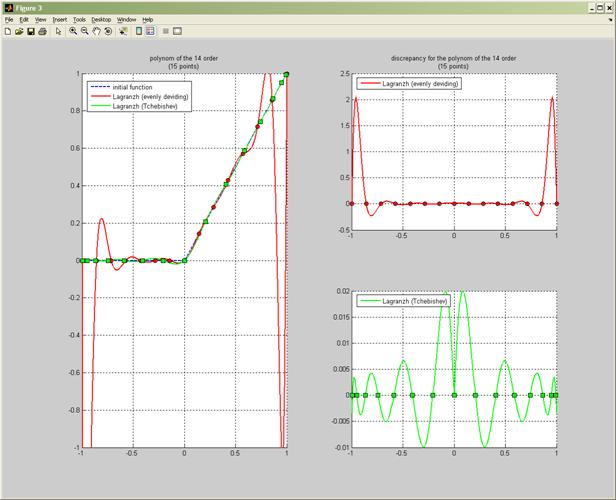
Выводы

• Метод выбора узлов Чебышева позволил минимизировать погрешность на всей области построения. Наблюдается характерное возрастание погрешности в середине области построения и ее убывание на концах области. Погрешность метода равномерного разбиения напротив возрастает на концах, убывает в середине области, но при этом имеет большие значения, чем погрешность метода Чебышева.
• Рассмотренные примеры показали, что многочлены 2, 6, 14 степеней дают погрешность, которой все же нельзя пренебречь при решении задачи, хотя погрешность полинома 14 степени с выбором узлов по Чебышеву составляет не более 0,02, что равно 0,02%.
• Если говорить о достоверности работы написанной мною программы, можно заметить что построенный двумя методами разбиения полином Лагранжа, в заданных узлах совпадает с исходной функцией, что хоть и не с большей степенью, но говорит о достоверности работы программы. Есть и другие методы проверки но мы не используем их в данной курсовой работе.