Эффективность и экономические оценки (Глава учебного пособия "Экономическая кибернетика"), страница 8

Целевая функция здесь имеет следующий вид:

«г

2. Теперь предположим, что вектор потребления (Ci, Сч) может строиться несколькими, например двумя, способами. Им соответствуют приведенные ниже матрицы коэффициентов баланса (11.10) (ради упрощения опустим ограничения на орудия труда и примем, что а,г=0):

Построим оптимальный план выпуска предметов потребления с интенсивностями, ограниченными снизу значениями Ci и Сд, при минимуме затрат труда. Запишем прямую задачу:

Из решения этой задачи найдем интенсивности каждого из способов производства, т. е. компоненты Z? и экстремальное значение целевой функции, выраженное через параметры модели и ограничения.

276

Оценки оптимального плана—в данном случае оценки компонент потребления—определяются из двойственной задачи, которая описывается следующей системой неравенств:

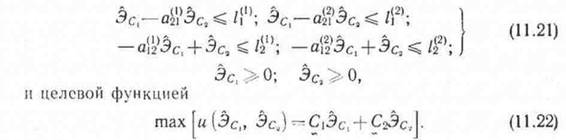
Две искомые оценки компонент потребления   Эс, и Эс,, имеющие в данном случае размерность затрат труда, связаны четырьмя неравенствами (11.21). Одновременно в строгие равенства могут быть обращены только два из них—одно из первой пары неравенств, другое—из второй. Можно показать, что строгие равенства будут иметь место для худшего из способов производства, попавших в оптимальный план. Его называют замыкающим. Все способы производства, попавшие в оптимальный план, трактуют как рентабельные.

3. Приведем теперь пример, на котором Л. В. Канторович иллюстрирует экономический смысл оценок ресурсов многократного использования. К таким ресурсам относятся, в частности, основные производственные фонды.

Данные табл. 11.1 характеризуют объемы пяти видов работ и себестоимости их выполнения при различных соотношениях между затратами ручного труда и использованием машин. При подсчете себестоимости учтены все эксплуатационные расходы, а также амортизация и ремонт оборудования. Имеется 100 машин, срок выполнения всех работ— 100 дней. Требуется выбрать способ выполнения каждого вида работ, обеспечивающий минимальную суммарную себестоимость.

На первый взгляд может показаться, что машины следует применять там, где они дадут наибольшее снижение себестоимости по сравнению с работой вручную, например, для работы

Ill вида, где эта себестоимость в семь раз ниже. Однако такое решение в действительности неправильное. Подсчитаем для каждого вида работ, насколько применение машин позволяет снизить общую себестоимость по сравнению с ручным трудом. Получаем для единицы работы I вида: 0,6—0,2=0,4 за машино-день: 1000-0,4=400 руб.; таким же образом для работы II вида—900 руб., для III—300, для IV—1000, для V— 600 руб. Отсюда ясно, что прежде всего следует машину применять на IV, затем на II, V, I и III видах работ. Для выполнения IV вида работы в 100 дней требуется 40 машин, для II —30, для V—50 машин. Следовательно, часть работ V вида и полностью работы I и III вида приходится выполнять вручную. Таким образом, получим оптимальный план, показанный в табл. 11.2.   

Таблица 11.2