

Тоэ
![]()
![]()
![]() 1)Схемы замещения электрических цепей и их параметры.Для
упрощения расчёта и анализа электрических цепей их заменяют схемами замещения,
составленными из отдельных элементов, математическое описание которых отражает
реальные процессы в электрической цепи. Резистивный элемент- преобразует
э/м энергию в тепло согласно закону Джоуля-Ленца: Тепловая энергия-(1), мощность
тепловой энергии-(2). На электрических схемах линейный резистивный элемент
обозначается прямоугольником имеет постоянное сопротивление в Омах и линейную
ВАх. Напряжение и ток резистивного элемента связаны между собой законом Ома U=φ1-φ2=RiR. Для
постоянного тока iR=IR. Для
гармонического тока iR(t)=Imsin(wt+β). В резистивном элементе синусоидальный ток и напряжение
совпадают по фазе. Индуктивный элемент-запасает э/м энергию в магнитном
поле(3). PL=ULi. Имеет
постоянную индуктивность и линейную Вебер-амперную характеристику (Ψ(i)=Li-потокосцепление).
Для линейного индуктивного элемента энергия запасаемая в магнитном поле WM=Li2/2. Напряжение
и ток индуктивного элемента связаны между собой законом электромагнитной
индукции UL=dΨ/dt=d(Li)/dt=Ldi/dt. При постоянном токе индуктивный элемент является
закороткой UL=0. При синусоидальном токе UL=wLIMcos(wt+β)=UMsin(wt+β+π/2). Гармоническое
напряжение на инд элементе опережает свой ток по фазе на 90º.Ёмкостной
элемент-запасает энергию в электрическом поле
1)Схемы замещения электрических цепей и их параметры.Для
упрощения расчёта и анализа электрических цепей их заменяют схемами замещения,
составленными из отдельных элементов, математическое описание которых отражает
реальные процессы в электрической цепи. Резистивный элемент- преобразует
э/м энергию в тепло согласно закону Джоуля-Ленца: Тепловая энергия-(1), мощность
тепловой энергии-(2). На электрических схемах линейный резистивный элемент
обозначается прямоугольником имеет постоянное сопротивление в Омах и линейную
ВАх. Напряжение и ток резистивного элемента связаны между собой законом Ома U=φ1-φ2=RiR. Для
постоянного тока iR=IR. Для
гармонического тока iR(t)=Imsin(wt+β). В резистивном элементе синусоидальный ток и напряжение
совпадают по фазе. Индуктивный элемент-запасает э/м энергию в магнитном
поле(3). PL=ULi. Имеет
постоянную индуктивность и линейную Вебер-амперную характеристику (Ψ(i)=Li-потокосцепление).
Для линейного индуктивного элемента энергия запасаемая в магнитном поле WM=Li2/2. Напряжение
и ток индуктивного элемента связаны между собой законом электромагнитной
индукции UL=dΨ/dt=d(Li)/dt=Ldi/dt. При постоянном токе индуктивный элемент является
закороткой UL=0. При синусоидальном токе UL=wLIMcos(wt+β)=UMsin(wt+β+π/2). Гармоническое
напряжение на инд элементе опережает свой ток по фазе на 90º.Ёмкостной
элемент-запасает энергию в электрическом поле

![]() энергия электрического поля (4). Имеет постоянную ёмкость и линейную
Кулон-Вольтную характкристику. Для линейного ёмкостного элемента запасаемая
энергия в электрическом поле Wэ=СU2C/2. Напряжение
и ток связаны между собой соотношением: i=dq/dt=d(cUC)/dt=CdUc/dt. При постоянном напряжении ёмкостный элемент является
разрывом i=0. При синусоидальном напряжении i(t)=CUMwcos(wt+α)=IMsin(wt+α+π/2). Гармонический ток опережает своё напряжение по
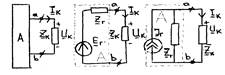
фазе на 900. Идеальный источник ЭДС-у которого напряжение на
его зажимах u=e при
любом генерируемом токе I, т.е. внутреннее
сопротивление идеального источника равно нулю. Генерируемая мощность Ре=ie. Вах идеального источника ЭДС имеет горизонтальный вид
не зависит от тока i. Идеальный источник тока-генерируемый
ток i равен задающему току J при любом напряжении u на его зажимах, т.е. внутреннее сопротивление источника
равно бесконечности. Генерируемая мощность источника тока РJ=uJ. Идеальный
ключ-используется для составления схем замещения реальных коммутирующих
устройств. Ключи замыкаются/размыкаются мнгновенно быстро, в замкнутом
состоянии R=0 а в разомкнутом R=бесконечности.
энергия электрического поля (4). Имеет постоянную ёмкость и линейную
Кулон-Вольтную характкристику. Для линейного ёмкостного элемента запасаемая
энергия в электрическом поле Wэ=СU2C/2. Напряжение
и ток связаны между собой соотношением: i=dq/dt=d(cUC)/dt=CdUc/dt. При постоянном напряжении ёмкостный элемент является
разрывом i=0. При синусоидальном напряжении i(t)=CUMwcos(wt+α)=IMsin(wt+α+π/2). Гармонический ток опережает своё напряжение по
фазе на 900. Идеальный источник ЭДС-у которого напряжение на
его зажимах u=e при
любом генерируемом токе I, т.е. внутреннее
сопротивление идеального источника равно нулю. Генерируемая мощность Ре=ie. Вах идеального источника ЭДС имеет горизонтальный вид
не зависит от тока i. Идеальный источник тока-генерируемый
ток i равен задающему току J при любом напряжении u на его зажимах, т.е. внутреннее сопротивление источника
равно бесконечности. Генерируемая мощность источника тока РJ=uJ. Идеальный
ключ-используется для составления схем замещения реальных коммутирующих
устройств. Ключи замыкаются/размыкаются мнгновенно быстро, в замкнутом
состоянии R=0 а в разомкнутом R=бесконечности.
2)Основные законы электрических цепей.Напряжение и ток резистивного элемента связаны между собой законом Ома.U1-2=φ1-φ2=IR*R. Если участок цепи содержит ЭДСкоторая направлена согласно с током то закон Ома выглядит: U1-2=IR*R-E если направлены встречно то U1-2=IR*R+E.Законы Кирхгофа справедливы для установившегося и переходного режима линейных и не линейных цепей при любых законах изменения во времени напряжения и токов. 1ЗК- для любого узла электрической цепи алгебраическая сумма токов равна нулю:∑±ik=0. Физически 1ЗК я вляется законом непрерывности электрического тока. 2ЗК- для любого контура электрической цепи алгебраическая сумма напряжений на пассивных элементах равна алгебраической сумме ЭДС и напряжений источников тока, действующих в этом контуре, со знаком «+» берутся те, положительное направление которых совпадает с направлением отхода контура ∑±UП=∑±ек+∑±Uq(J).
 3)Законы Кирхгофа их применение для расчёта
установившегося режима линейных резистивных электрических цепей. Законы
Кирхгофа справедливы для установившегося и переходного режима линейных и не
линейных цепей при любых законах изменения во времени напряжения и токов. 1ЗК-
для любого узла электрической цепи алгебраическая сумма токов равна нулю:∑±ik=0. Физически 1ЗК я вляется законом непрерывности
электрического тока. Для схемы с nу узлами
по 1ЗК можно составить n1= nу-1 независимые уравнения которые в
матричной форме имеют вид:[А]*[ik]=0. Где
А-узловая матрица (таблица коэффициентов перед токами), токи соответствуют
узлам, столбцы токам), ik-матрица
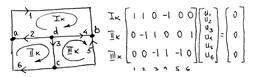
столбец токов в схеме. Для графосхемы с nу=4
составляем n1= nу-1=4-1=3
уравнений по 1ЗК. Узел d принимаем
за базисный. Для узла а:I1-I2-I6=0,b:-I1-I3+I4=0, c: I2+I3-I5=0.
3)Законы Кирхгофа их применение для расчёта
установившегося режима линейных резистивных электрических цепей. Законы
Кирхгофа справедливы для установившегося и переходного режима линейных и не
линейных цепей при любых законах изменения во времени напряжения и токов. 1ЗК-
для любого узла электрической цепи алгебраическая сумма токов равна нулю:∑±ik=0. Физически 1ЗК я вляется законом непрерывности
электрического тока. Для схемы с nу узлами
по 1ЗК можно составить n1= nу-1 независимые уравнения которые в
матричной форме имеют вид:[А]*[ik]=0. Где
А-узловая матрица (таблица коэффициентов перед токами), токи соответствуют
узлам, столбцы токам), ik-матрица
столбец токов в схеме. Для графосхемы с nу=4
составляем n1= nу-1=4-1=3
уравнений по 1ЗК. Узел d принимаем
за базисный. Для узла а:I1-I2-I6=0,b:-I1-I3+I4=0, c: I2+I3-I5=0.
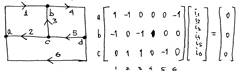 2ЗК- для любого контура электрической цепи алгебраическая
сумма напряжений на пассивных элементах равна алгебраической сумме ЭДС и
напряжений источников тока, действующих в этом контуре, со знаком «+» берутся
те, положительное направление которых совпадает с направлением отхода контура
∑±UП=∑±ек+∑±Uq(J). Для
схемы с nу узлами и nв ветвями по 2ЗК можно составить n2=nв-n1 уравнений, которые в матричной форме имеют
вид [B]*[Uk]=0. В-контурная
матрица (таблица коэфициентовперед напряжениями ветвей схемы строки –контуры,
столбцы-ветвям). Uk=матрица
столбец напряжений ветвей схемы. Для графосхемы с nу=4, nв=6 составляем n2=nв-n1=6-3=3 уравнения
которые представлены в матричной форме.
2ЗК- для любого контура электрической цепи алгебраическая
сумма напряжений на пассивных элементах равна алгебраической сумме ЭДС и
напряжений источников тока, действующих в этом контуре, со знаком «+» берутся
те, положительное направление которых совпадает с направлением отхода контура
∑±UП=∑±ек+∑±Uq(J). Для
схемы с nу узлами и nв ветвями по 2ЗК можно составить n2=nв-n1 уравнений, которые в матричной форме имеют
вид [B]*[Uk]=0. В-контурная
матрица (таблица коэфициентовперед напряжениями ветвей схемы строки –контуры,
столбцы-ветвям). Uk=матрица
столбец напряжений ветвей схемы. Для графосхемы с nу=4, nв=6 составляем n2=nв-n1=6-3=3 уравнения
которые представлены в матричной форме.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.