Схемы замещения электрических цепей и их параметры. Законы Кирхгофа их применение для расчёта установившегося режима линейных резистивных электрических цепей. Законы Ома и Кирхгофа в комплексной форме, страница 6

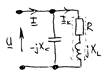
R=R_K+R_Н φ=arctg((X_L-X_C)/R) , тогда по закону Ома I=U/Z_ВХ=Ue^j(α-φ)/Z_ВХ Исходя из определения резонанса имеем φ=0, следовательно условием резонанса напряжений будет X_L-X_C=0 (X_L=X_C ;WL=1/WC или W²LC=1). В результате резонанс напряжений может быть достигнут изменением w,L,C. С=С_РЕЗ=1/W²L=1/WX_L- резонансная ёмкость. При резонансе напряжений имеем: ZВХ=R=R_K+R_Н ;Х=X_L-X_C=0; φ=0;  I= Ue^jα/R; P=UIcosφ=U²/R(Вт); Q=UIsinφ=0(ВАР); S=(P²+Q²)^1/2=P (Вт). Т.е. в режиме резонанса цепь потребляет максимально возможную активную мощность, равную полной мощности. В режиме резонанса напряжений за счёт взаимной компенсации реактивных сопротивлений входное сопротивление цепи минимально и равно R=Z_ВХ. Резонанс токов- при параллельном соединении ёмкости и индуктивности.                                     По   закону Ома:  I=U/Z_ВХ=Ie^j(α-φ); U_ВХ=Ue^jα ; Z_ВХ=Ze^jα определение входной проводимости:

Y_ВХ=1/Z_ВХ=Y_C+Y_K=1/(-jX_C)+(1/(R+jX_L)=j/X_C+(R-jX_L)/((R+jX_L)(RjX_L))=     

j/X_C+(R-jX_C)/(R²+X_L²)+j[1/X_C+X_L/(R²+X_L²)]=g-jb=Y_ВХe^-jφ ,где Y_ВХ=(g²+b²)^1/2 (Ом^-1)-модуль входной проводимости. G= R/(R²+X_L²) (Ом^-1)-активная проводимость; b=b_K-b_C(Ом^-1)-реактивная проводимость; b_K= X_L/(R²+X_L²) (Ом^-1)-индуктивная проводимость. b_C=1/Х_с (Ом^-1)-ёмкостная проводимость; φ=arctg(b/g)-угол сдвига фаз между входным напряжением и током. При резонансе φ=0 b=b_K+b_C=0 т.е.  X_L/(R²+X_L²)=1/X_c-условие резонанса токов. Т.е. резонанс токов может быть достигнут изменением W,L,C,R. Так результирующая ёмкость

С_РЕЗ=L/(R²+X_L²). Следовательно при резонансе токов имеем Y_ВХ=g; Y=0; I=UY_ВХ=Uge^jα; P=UIcosφ=U²g(Вт); Q=UIsinφ=0(ВАР); S=(P²+Q²)^1/2=P=U²g (ВА). За счёт взаимной компенсации реактивных составляющих проводимостей b_C и b_K входная проводимость цепи будет вещественна и минимальна, следовательно входной ток при резонансе токов будет минимальным I=UY_ВХ=Uge^jα. При этом токи в ёмкости и катушке(I_C ;I_K) могут значительно превосходить по величие входной ток I. Резонанс в сложной цепи- отличается тем что C и L включены между собой не параллельно и не последовательно. Пример: По закону Ома I_L=U/Z_ВХ=Ue^j(α-φ)/Z_ВХ ; U_ВХ=Ue^jα

Z_ВХ=jX_L+(R(-jX_c))(R-jX_c)=

j+(R(-jX_c))(R+jX_c)/(R(-jX_c))(R+jX_c))=  jX_L+(R(-jX_c))(R+jX_c)/(R²+X_c²)=RX_C²+j(X_L-RX_C²/(R²+X_c²)=R_ВХ+jX_ВХ; R_ВХ=RX_C²/(R²+X_c²)(Ом) –активная составлющая входного сопротивления; X_ВХ=(X_L-RX_C²/(R²+X_c²)(Ом)- реактивная составляющая входного сопротивления. Z_ВХ= (R_ВХ²+jX_ВХ²)^1/2 (Ом)- модуль входного сопротивления. φ=arctg(X_ВХ/ R_ВХ)-угол сдвига фаз. При резонансе φ=0, X_ВХ=0, т.е. X_L=RX_C²/(R²+X_c²), Z_ВХ= R_ВХ=RX_C²/(R²+X_c²), I_L=U/Z_ВХ=Ue^jα/R_ВХ; P=UIcosφ=U²/ R_ВХ (Вт); Q=UIsinφ=0(ВАР); S=(P²+Q²)^1/2=P

18)Расчёт симметричного режима линейных трёхфазных цепей с гармоническими (синусоидальными) напряжениями и токами. Симметричный режим-такой режим, когда напряжения и токи фаз образуют симметричные системы и нагрузка фаз одинакова. Расчёт симметричного режима ведётся символическим методом на одну фазу с использованием законов Кирхгофа и Ома. При этом падение напряжения в обмотках генераторов и трансформаторов обычно принебрегают и представляют эти обмотки в виде наводимых в них фазных ЭДС. Е_А, Е_В, Е_С. 1)Соединение звезда-звезда с нулевым проводом. Дано Е_А=Ее^jα, Е_В==Ее^j(α-120), Е_С=Ее^j(α+120), -Симметричная система фазных ЭДС. Z=Ze^jα- сопротивление напряжения фазы. Z_N=Ze^jα- cопротивление в нулевом проводе. Найти I_A, I_B, I_C- линейные токи которые равны фазным токам. U_А, U_В, U_С-фазные напряжения нагрузки. I_N – ток в нулевом проводе. U_N- напряжение смещения нейтрали. а) Линейные токи: I_А=Е_А/Z=Еe^j(α-φ)/Z=I_А e^j(α-φ), гдеI_А=Е_А/Z-действующее значение.

I_В=а²I_А= I_А e^j(α-φ-120); I_С=аI_А= I_А e^j(α-φ+120) б) ток в нулевом проводе I_N=I_А+I_В+I_С.

в)фазные напряжения U_А=I_АZ_А=Е_А ; U_В=а²U_А=Е_В, U_С= аU_А=Е_С, U_Ф=Е-действующее значение фазных напряжений. г)Напряжение смещения нейтрали U_N=I_NZ_N=0. д)Мощность трёх фаз: S_b=E_AI_A*+E_BI_B*+E_CI_C*+=3EI_лe^jφ=Pb+Qb (ВА). S_b=EI_Л ; Uл=3^1/23^1/2E; P_n=P_b=3I_Л²Re(Z)=3I_ЛU_Фcosφ=3^1/2I_лU_лcosφ (Вт); Q_n=Q_в=3I_Л²I_msinφ (ВАР). Т.к. U_N=0 и I_N=0  то расчёт трёхфазной цепи соединённой звездой без нулевого провода ведётся аналогично. 2)Соединение нагрузки Z_N=Ze^jφ в треугольник при заданной системе линейных напряжений. U_AB=U_Лe^jλ; U_AB=а²U_АВ; U_СА=аU_АВ. При помощи законов Ома и Кирхгофа определяют: а)фазные токи I_АВ=U_АB/Z= U_лe^j(λ-φ)/Z=I_Фe^j(λ-φ); I_ВС=а²I_АВ; I_СА=аI_АВ I_Ф==U_Л/Z; I_А=I_АВ- I_СА=(1-a)I_АВI_Л^λ-φ-30)