Схемы замещения электрических цепей и их параметры. Законы Кирхгофа их применение для расчёта установившегося режима линейных резистивных электрических цепей. Законы Ома и Кирхгофа в комплексной форме, страница 2

4)Символический метод расчёта установившегося режима линейных электрических цепей с гармоническими напряжениями и токами. Применяется для расчёта установившегося режима в линейных цепях с гармоническими напряжениями и токами. Метод основывается на изображении вращающегося вектора на комплексной плоскости. Синусоидальную величину f(t)=F_Msin(wt+α) можно изобразить на комплексной плоскости в виде вращающегося вектора который можно записать в тригонометрической, показательной или алгебраической формах: F_Me^j(wt+α)=F’_M+jF”_M=F_Mcos(wt+α)+jF_Msin(wt+α)=a+jb=IM[F_Me^j(wt+α)]= IM[F_Me^jwt]. j=(-1)^0.5-мнимая единица; F’_M-проекция на вещественную ось; F”_M-проекция на мнимую ось. F_M=F_Me^jα-комплексная амплитуда.Комплекс действующего значения F=F_M/2^0.5=Fe^jα. Для расчёта символичским методом изображаются комплексная схема замещения в которой резистивные элементы R остаются без изменения индуктивные элементы заменяются комплексным сопротивлением Z_L=jX_L ёмкостные Z_C=-jX_C, а источники энергии заменяются их комплексами действующих значений ЭДС и токов.

5)Законы Ома и Кирхгофа в комплексной форме. Закон Ома выполняется для комплексов амплитуд(напряжений)или комплексов действующих значений I_m=U_m/Z; I=U/Z. Для резистивного элемента U_R(t)=U_RMsin(wt+β),U_R=RI(вектора напряжений и токов совпадают по фазе). Для индуктивного элемента U_L(t)=U_LMsin(wt+β+90⁰), U_L=jwLI=U_Le^j(β+90)(напряжение опережает ток на 90⁰). Для ёмкостного элемента U_C(t)=U_CMsin(wt+β-90),U_C=I/jwC=-jX_cI=U_Ce^j(β-90) (напряжение отстаёт от тока на 90⁰). 1ЗК-для любого узла комплексной схемы замещения алгебраическая сумма комплексов действующих значений токов равна нулю:∑±I_k=0. 2ЗК-для любого контура комплексной схемы замещения алгебраическая сумма комлексов действующих значений напряжения пассивных элементов в цепи равна алгебраической сумме комплексов действующих значений ЭДС и напряжений источников тока в данном контуре, а также равна алгебраической сумме комплексов действующих значений напряжений между точками разрыва данного контура:∑±U_п=∑±Е_к+∑±U_q^J+∑±U_R. По 1ЗК составляется n₁= n_у-1 уравнений. По 2ЗК n₂=n_в-n₁ уравнений.

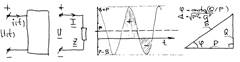6)Активная, реактивная и полная мощности при гармонических напряжениях и токах. Коэффициент мощности. Пусть на входе двухполюсника имеем U(t)=2^0.5Usin(wt+α) и i(t)=2^0.5Isin(wt+β), тогда мгновенная мощность функции времени на входе у двухполюсника P(t)=U(t)i(t)=2UIsin(wt+α)sin(wt+β)= =2UI[0.5cos(α-β)-0.5cos(2wt+α+β)]=P-Scos(2wt+α+β), где P=UIcosφ=[Вт]-средняя активная мощность, φ=α-β- сдвиг фаз между U и I, S=UI=[ВА]- полная (кажущаяся) мощность, cosφ=P/S≤1- коэффициент мощности, P(t) изменяется с двойной угловой частотой 2w по сравнению с напряжением и током, и в те моменты, когда P(t)>0, энергия поступает в двухполюсник из внешней цепи, а когда P(t)<0, энергия из двухполюсника отдается во внешнюю цепь. Представив двухполюсник комплексным сопротивлением Z=R+jX=Ze^jφ, для комплексов действующих значений тока I=Ie^jβ и напряжений U=Ue^jα, комплекс полной мощности S=UI^*=Ue^jα(Ie^-jβ)=UI^ej(α-β)=UI^ejφ=[Scosφ+jSsinφ]=P+jQ. P=Scosφ=UIcosφ=[Вт]- активная мощность, Q=Ssinφ=UIsinφ=[ВАр]- реактивная мощность. Активная мощность P=I²R является мощностью тепловой энергии, а реактивная Q=I²X пропорциональна максимальному значению энергии, запасаемой в электромагнитном поле.

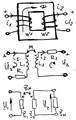7)Сущность и применение метода контурных токов при постоянных и гармонических токах. Применяется для расчета сложных линейных схем с постоянными или гармоническими напряжениями и токами (с одинаковой w). Метод используется с целью уменьшения числа решаемых уравнений, по сравнению с законами Кирхгофа. Сущность метода в введении в расчет контурных токов- фиктивные расчетные токи, замыкающиесяв независимых замкнутых контурах цепи, которые отличаются друг от друга наличием хотя бы одной новой ветви. Общий вид уравнения для контурного тока I_kk: Z_kkI_kk+∑±Z_kmI_mm=E_kk, где Z_kk- сопротивление k-го контура, равное сумме сопротивлений этого контура, I_kk- контурный ток k-го контура, Z_km- смежное сопротивление между k-м и m-м контурами, I_mm- сосоедний контурный ток в m-м контуре, + ставится когда  I_kk и I_mm напрвлены в одну сторону Z_km, E_kk- контурная ЭДС в k-м контуре = алгебраической ЭДС этого контура, с + берутся те, направление которых совпадает с направлением I_kk. При направлении  контурных токов необходимо учитывать: через источник тока должен проходить один контурный ток, который равен току источника тока; для контурного тока, проходящего через источник тока, контурный ток не составляется. Число контурных токов: n_кт=n_в-n_у+1, число контурных уравнений n_ку=n_i-n_у+1, где n_i– число неизвестных токов. Для резистивных цепей с постоянными токами контурные уравнения составляются аналогично (R вместо Z).