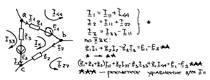Схемы замещения электрических цепей и их параметры. Законы Кирхгофа их применение для расчёта установившегося режима линейных резистивных электрических цепей. Законы Ома и Кирхгофа в комплексной форме, страница 3

8)Сущность и применение метода узловых потенциалов при постоянных и гармонических токах. Применяется для расчета линейных цепей с постоянными или гармоническими напряжениями и токами, наиболее удобен когда число узлов значительно меньше числа контуров. Расчетные уравнения этого метода доказываются при помощи 1ЗК и обобщенного закона Ома. По обобщенному закону Ома: I₁=(φ_a-φ_c+E₁)/Z₁=(φ_a-φ_c+E₁)Y₁; I₂=(φ_a-φ_b)/Z₂=(φ_a-φ_b)Y₂; по 2ЗК: -J+I₁+I₂=0;      -J+(φ_a-φ_c+E₁)Y₁+(φ_a-φ_b)Y₂=0; расчетное уравнение для узла a:               (Y₁+Y₂)φ_a-Y₂φ_b-Y₁φ_c=J-E₁Y₁. В общем виде для k-го узла: Y_kkφ_k-∑Y_kmφ_m=I_k^(у) где Y_kk-узловая проводимость k-го узла = сумме проводимостей ветвей, подходящих к данному узлу (проводимость с источником тока равна нулю); φ_k- потенциал k-го узла; Y_km-проводимость ветви, соединяющей m-й и k-й узлы; φ_m– потенциал соседнего m-го узла. Узловой ток k-го узла: I_K^(у)=∑±E_qY_q+∑±J_q равный алгебраической сумме произведений ЭДС подходящих к к-му узлу на проводимости своих ветвей к алгебраической сумме подходящих к к-му узлу токов источников. Причём, с «+» берутся те у которых ЭДС и токи источников направлены в к-й узел. Потенциалы определяются с точностью до постоянной. Потенциал некоторого узла схемы может быть принят равным 0. Обычно за такой узел берётся такой, который соединён с землёй     или с корпусом прибора или узел ветви, содержащий только один источник ЭДС. Таким образом по методу узловых патенциалов можно составить: n_м.у.п.≤n_у-1 узловых уравнений. После расчёта узловых патенциалов по обобщённому закону Ома находятся токи ветвей схемы.

9)Сущность и применение метода наложения при постоянных и гармонических токах. Применим к линейным цепям и основан на принципе наложения. Любой ток/напряжение равен алгебраической сумме частичных токов/напряжений, создаваемым каждым источником в отдельности. Метод наложения основывается на определении частичных токов/напряжений любыми из известных методов. Порядок расчёта метода наложения линейных цепей с постоянными или гармоническими напряжениями или токами: 1)исходная схема (комплексная или резистивная) разбивается на ряд подсхем, в каждой из которых действует один источник ЭДС или один источник тока. Остальные источники ЭДС закорочены, а ветви с остальными источниками тока разорваны. 2)Любыми известными рассчитываются напряжения подсхем и определяются частичные токи и напряжения.3)Результирующие напряжения и токи исходной схемы определяются алгебраические суммы частичных величин, при этом с «+» берутся те частичные величины, направления которых совпадают с направлением результирующего тока или напряжения. Пример: Дано: E₁,E₂,J,Z₁,Z₃,Z₄,Z₅. Найти I₅.

1)Расчёт подсхем.

Схема (а): Подсхема с ЭДС Е₁. По закону Ома: I₁⁽¹⁾=E₁/Z_Э1=E₁/(Z₁+Z₅(Z₃+Z₄)/(Z₅+(Z₃+Z₄))). По правилу распределения токов: I_Б⁽¹⁾=I₁⁽¹⁾*(Z₃+Z₄)/(Z₅+(Z₃+Z₄)). Посхема (б) с ЭДС Е₂: I₂⁽²⁾=E₂/Z_Э2=E₂/(Z₁+Z₅(Z₃+Z₄)/(Z₅+(Z₃+Z₄))). I₅⁽²⁾=I₂⁽²⁾*(Z₃+Z₄)/(Z₅+(Z₃+Z₄)). Подсхема с J: I₁₁=J для I₂₂: I₂₂(Z₃+Z₄+Z₅)+I₃₃Z₅-I₁₁Z₃=0 для I₃₃: I₃₃(Z₁+Z₅)+I₂₂Z₅=0 I₅⁽³⁾=I₂₂+I₃₃ окончательный результат: I5=I₅⁽¹⁾-I₅⁽²⁾+I₅⁽³⁾

10)Сущность и применение метода эквивалентного генератора(источника активного двухполюсника) при постоянных и гармонических(синусоидальных)токах. Применяются для анализа и расчёта линейных резистивных цепей с постоянными токами и комплексных схем замещения с гармоническими токами.

А-активный двухполюсник-цепь имеющая два выхода на зажимах (а и в) и содержащая источники ЭДС и тока. Е_Г=U_K^XX-ЭДС активного источника (генератора), равная напряжению хх, когда Z_K=бесконечности и I_K=0. Z_Г=Z_ОВ-эквивалентное сопротивление активного двухполюсника относительно зажимов а и в, когда ЭДС активного двухполюсника закорочены а ветви источников тока разорваны. J_Г=E_Г/Z_Г=I_К^КЗ-задающий ток эквивалентного источника питания равный току короткого замыкания между зажимами а и в, когда Z_К=0, U_K=0. Теорема: Любой линейный активный двухполюсник можно заменить эквивалентным источником тока соответственно равными ЭДС-напряжению холостого хода, задающий ток-току короткого замыкания между а и в. На основании этой теоремы реализован метод расчёта тока в некоторой ветви схемы (I_К), который называется методом эквивалентного генератора, ток (I_К) будет равен: I_K=E_Г/(Z_Г+Z_K)=J_ГZ_Г/(Z_Г+Z_K)=J_Г/(1+Z_K/Z_Г).