Основы теплообмена. Основные способы передачи тепла. Теплопроводность, страница 7

Тело, пропускающее сквозь себя  всю лучистую энергию, называется диатермичным (абсолютно прозрачным);  для него D = 1, R = A = 0.  

В природе абсолютно черных, прозрачных, белых тел нет.

3.6.2. Закон Стефана-Больцмана

Количество энергии, излучаемое абсолютно черным телом пропорционально четвертой степени температуре, измеренной в градусах Кельвина:

                                                E_O = s_oT⁴,                                               (3.24)

E_o – лучеиспускательная способность абсолютно черного тела, Вт/м²; s_o -  5,67×10^-8 Вт/(м²×K⁴) – константа излучения абсолютно черного тела; [T]= K. В технических расчетах при больших температурах пользуются уравнением:

                                          E_O = C_O(T/100)⁴                                            (3.25)

С_O = s_o×10⁸ = 5,67 Вт/(м²×K⁴)   - коэффициент лучеиспускания абсолютно черного тела.

Закон Стефана-Больцмана можно применить к серым телам. Под серыми телами понимаются такие тела, спектр излучения  которых подобен спектру излучения абсолютно черного тела и отличается  от него только тем, что при одной и той же температуре каждая ордината интенсивности излучения серого тела составляет  одну и ту же долю  от сходственной ординаты абсолютно черного тела.

Для серого тела имеем:

                                       E = C (T/100)⁴ .                                         (3.26)

E – лучеиспускательная способность серого тела, Вт/м²;  C – коэффициент лучеиспускания серого тела,   Вт/(м²×K⁴).

Степень черноты серого тела:

                                      e = E/E_O = C/C_O .                                      (3.27)     

Степень черноты  e изменяется от 0 до 1. На основании изложенного выше можем получить;

                                    E = eE_O = eC_O(T/100)⁴.                               (3.28)

3.6.3. Закон Кирхгофа

Закон устанавливает связь между излучательной  и поглощательной способностями любого тела.

Отношение лучеиспускательной способности  E  к поглощательной A одинаково для всех тел и равно лучеиспускательной способности абсолютно черного тела при той же температуре и зависит только от температуры:

                                    E/A = E_O = C_O(T/100)⁴ .                           (3.29)           

Так как E/E_O = e,    то A = e. На основании формулы (3.27) имеем;

                                              C/A = C_O .                                            (3.30)

В соответствии с законом Кирхгофа – чем больше поглощательная способность тела, тем больше  и излучательная способность, и наоборот, чем меньше энергии способно тело  получать при данной температуре, тем меньше оно способно и поглощать.

3.6.4. Закон Ламберта

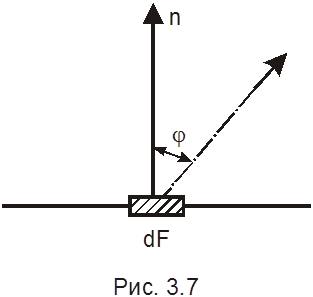
Он устанавливает, что излучательная способность тела с единицы поверхности в каком-либо направлении пропорционально косинусу угла между этим направлением и нормалью к поверхности  ( см. рис. 3.7):

                                         E_j = E_ncosj ,                                           (3.31)

где E_п  = E/p -  излучение тела только в направлении нормали. Следовательно,

                              E_n = (e/p)C_O(T/100)⁴cosj.                             (3.32)

Закон Ламберта справедлив для абсолютно черных тел, для серых тел  он справедлив при j £ 60°.

3.6.5. Закон  Планка

Планк теоретически  вывел закон распределения энергии, излучаемой абсолютно черным телом, в зависимости от длин волн:

                             E_ОЛ = C₁l^-5(e^C/lT – 1)^-1, Вт/м³;                            (3.33)

E_ОЛ – спектральная интенсивность излучения абсолютно черного тела; l - длина волны, м; T – абсолютная температура тела, К:

С₁ – 3,68×10^-16 Вт×м²;    С = 1,67×10² м×К.

Графически закон Планка  представлен на рис. 3.8. Из рисунка видно, что интенсивность излучения с увеличением длины волны сначала резко возрастает, достигает  максимума при определенном значении l и затем уменьшается.

3.6.6. Закон Вина