Условие задачи. Определить площадь поверхности нагрева и число секций водоводяного теплообменника типа труба в трубе (рис. 3.14). Греющая вода движется по внутренней стальной трубе (lc для стали 45 Вт/(м×°С)) диаметрами d2/d1 = 35/32 мм и имеет температуру на входе .tж1’ = 95°С. Расход греющей воды G1 = 2130 кг/ч.
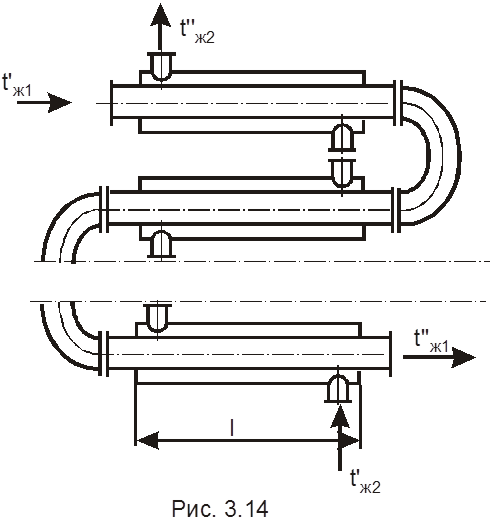
Нагреваемая вода движется противотоком по кольцевому каналу между трубами и нагревается от t’ж2= 15°С до t’’ж2 = 45°С. Внутренний диаметр внешней трубы D = 48 мм. Расход нагреваемой воды G2 = 3200 кг/ч. Длина одной секции теплообменника l = 1,9 м. Потерями теплоты через внешнюю поверхность теплообменника пренебречь. Принять давление сред 0,1 МПа.
Решение.
Удельная массовая теплоемкость воды »4,19 кДж/(кг×°С). Количество передаваемой теплоты:
Q = G2cp2 (t’’ж2 – t’ж1) = (3200/3600) 4,19 (45 – 15) = 111кВт.
Температура греющей воды на выходе:
t''ж1 -= t'ж1 – (Q/(G1cp1) = (111×3600)/(2130×4,19) = 50°С.
Находим среднеарифметические значения температур теплоносителей и значения физических свойств воды при этих температурах, используя таблицы термодинамических свойств воды и водяного пара:
tж1 = 0,5(t'ж1 + t''ж1) = 0,5(95 +50) = 72,5°С;
плотность r;ж1 = 976 кг/м3; коэффициент кинематической вязкости nж1 = mж1/rж1 = 0,403×10-6 м2/с; коэффициент теплопроводности lж1 = 0,679 Вт/(м×°С); критерий Прандтля Prж1= 2,47;
tж2 = 0,5(t’ж2 + t’’ж2) = 0,5(15+45) = 30°С; r;ж2= 996 кг/м3; nж2 = mж2/rж2= 0,805×10-6м2/с; lж2= 0,618 Вт/(м×°С); Prж2 = 5,42.
Скорости движения теплоносителей:
w1 = 4G1/(r;ж1 pd123600) = 4×2130/(976×3,14(3,2×10-2)2×3600) = 0,765 м/с;
w2=4G2( r;ж2p(D2 – d22) 3600 = 4×3200/(996×3,14(4,82 – 3,52) 10-4×3600) = 1,06 м/с.
Число Рейнольдса для потока греющей воды:
Reж1= w1d1/nж1= 0,755× 3,2×10-2/(0,403×10-6) = 6×104.
Режим течения греющей воды турбулентный. Расчет числа Нуссельта ведем по формуле (3.17):
Nuж1 = 0,021Re0,8ж1 Pr0,43Ж1(Prж1/Prc1)0,25, так как температура стенки неизвестна, то в первом приближении задаемся значением:
tс1 » = 0,5(tж1 + tж2) = 0,5(72,5 + 30) = 51,2 °С;
при той же температуре Prс1 = 3,5, тогда
Nuж1= 0,021(6×104)0,8 (2,47)0,43 (2,47/3,5)0,25 = 188.
Коэффициент теплоотдачи от греющей воды к стенке трубы:
a1 = Nuж1(lЖ1/d1) = 188(0,670/(3,2×10-2) =3940 Вт/(м2×°С).
Число Рейнольдса для потока нагреваемой среды:
Reж2=dэ w2/nж2 = 1,06×1,3×10-2/(0,805×10-6) = 1,71×104.
Эквивалентный (гидравлический) диаметр:
dэ = 4F/U = 4 (p(D2 – d22)/4)/(p(D + d2)) = 48 – 35 = 13 мм.
Режим течения нагреваемой воды турбулентный и расчет числа Нуссельта ведем по формуле для кольцевых каналов:
Nuж2 = 0,017Re0,8ж2 Pr0,4Ж2(Prж2/Prc2)0,25(D/d2)0,18.
Принимая в первом приближении tc2 » tc1, следовательно, Prc2 » Prc1 »3,5, получим:
Nuж2 = 0,017(1,71× 104)0,8(5,42)0,4(5,42/3,5)0,25(48/35)0,18 = 95.
Коэффициент теплоотдачи от стенки трубы к нагреваемой воде:
a2 = Nuж2(lж2/dэ) = 95 (0,618/(1,3 ×10-2)) = 4500 Вт/(м2×°С).
Коэффициент теплопередачи:
K = 1´ (1/a1 + dc/lc + 1/a2)-1 = 1´(1/3940 + 1/(1,5×10-3/45) + 1/4500)-1 = 1970 Вт/(м2×°С).
При противотоке имеем Dtб = 95 – 45 = 50°С; Dtм = 50 – 15 = 35 °С;
Тогда среднелогарифмическая разность температур:
Dt = (Dtб - Dtм)/ln (Dtб/Dtv) = (50 – 35)/ln(50/35) = 42,055 °С.
Удельная мощность теплового потока:
q = K×Dt = 1970 ×42,055 = 8,285×104 Вт/м2.
Площадь поверхности нагрева:
F = Q/q = 111/82,85 = 1,34 м2.
Число секций:
n = F/(pd12 ) = 1,34/(3,14 ×3,2×10-2× 1,9) » 7.
Средние температуры поверхностей стенок трубы:
tc1 = tж1 - q/a1 =72,5 - 82850/3940 = 51,б4°С;
tс2 = tж2 + q/a2 = 30 + 82850/4500 = 48,6°С.
Тогда Prc1 = 3,476 и Prc2 = 3,68 и поправки на изменение физических свойств жидкости по сечению потока имеют значения:
(Prж1/Prc1)0,25= (2,47/3,476)0,25 = 0,918 (в расчетах было принято 0,92);
(Prж2/Prc2)0,25 = (5,42/3,68)0,25 = 1,102 (в расчетах было принято 1,12).
Совпадение достаточно точное; можно принять F = 1,34 м2.
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.