Основы теплообмена. Основные способы передачи тепла. Теплопроводность, страница 2

Уравнение теплопроводности (уравнение закона Фурье) для слоя  dx (рис. 3.2) запишется в следующем виде:

q = - l ;

далее получаем:

dt = (q/l)dx.

После интегрирования:

t = - (q/l)x +C.

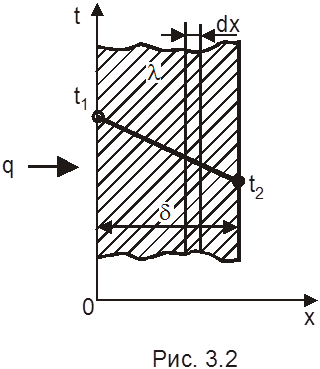
При x = 0    t = t₁, следовательно,  С = t₁.

t = - (q/l)x + t₁.                                       (3.4)

При x = d      t= t₂; после подстановки и преобразований получаем окончательно:

q = (l/d)(t₁ – t₂) .                                    (3.4)

3.3.4. Теплопроводность многослойной стенки

Предположим, что имеем трехслойную плоскую стенку бесконечной длины. В пределах каждого слоя коэффициент теплопроводности есть постоянная величина и не зависит от температуры и для каждого слоя обозначим

Таблица 3.1

Материалы	Коэффициент теплопроводности l, Вт/(м×град)
Газы
Воздух, t= 0¸ 1000°С при  p = 1бар	0,02¸0,075
Углекислота, t = 0 ¸ 600°С при p = 1 бар	0,014¸0,065
Метан, t = 0 ¸ 600°С  при  p = 1 бар°	0,031¸0,154
Жидкость
Вода, t = 0 ¸ 100°С	0,15¸0,29
Металлы
Алюминий	210
Чугун ( 3% С)  при  20°С	56 ¸ 65
Сталь  (0,2% С) при 20°С	48
Медь	380¸400
Латунь	116¸175
Серебро	420
Огнеупоры и строительные материалы
Карборундовые изделия	0,21-0,009tср
Кирпич динасовый	093+0,0006tср
Кирпич шамотный	0,32+0,0005tср
Шлакобетон набивной	0,7
Бетон с каменным щебнем	1,27
Кладка из красного кирпича	0,62¸0,82
Дерево	0,2¸0,4
Теплоизоляционные материалы
Асбест	0,088+0,00021tср
Зонолит	0,072+0,00025tср
Совелит	0,091+0,000075tср
Диатомит молотый	0,091+0,00024tср
Диатомитовый кирпич	0,113+0,0002tср
Минеральная вата	0,023¸0,046
Загрязнения на трубах
Накипь	0,023¸0,082

l₁,  l₂,  l₃; толщину каждого слоя  d₁, d₂, d₃; температуру на поверхности и границах слоев t₁, t₂, t₃, t₄ (см. рис. 3.3), t₁>t₂>t₃>t₄ .Передача тепла осуществляется в направлении оси x.

Для каждого слоя можем записать:

q=  (l₁/d₁)(t₁ - t₂);

q =  (l₂/d₂)(t₂ – t₃);

q =  (l₃/d₃)(t₃ – t₄).

Преобразуем и складываем:

(t₁ - t₂) = q (d₁/l₁);

(t₂ – t₃) = q (d₂/l₂);

(t₃ – t₄) = q (d₃/l₃);

-----------------------------

(t₁ – t₄) = q (d₁/l₁ +  d₂/l₂ + d₃/l₃).

q = 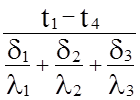, Вт/(м²×град).                              (3.5)

R = d₁/l₁ +  d₂/l₂ + d₃/l₃,

R- термическое сопротивление многослойной стенки.

q =  (t₁ – t₄)/R.                                                  (3.6)

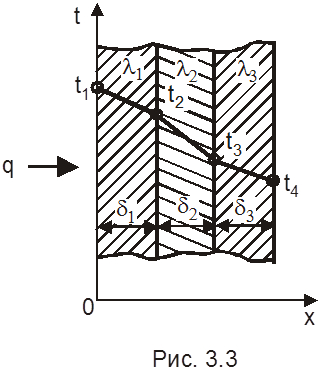
3.3.5 Теплопроводность цилиндрической стенки (трубы)

Имеем цилиндрическую стенку длиной l, внутренний радиус r_1,, наружный радиус r₂, коэффициент теплопроводности материала стенки l постоянен по всей стенке и не зависит от температуры, r – произвольный радиус (рис. 3.4).

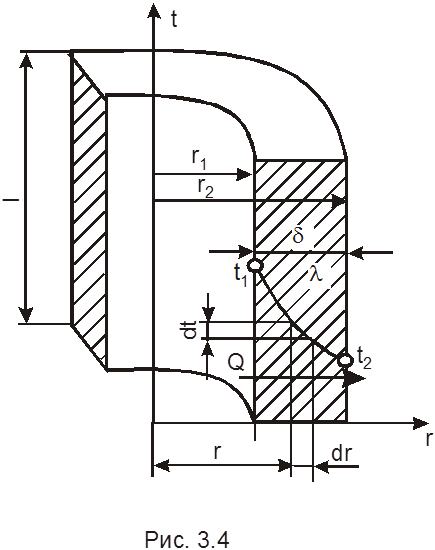
Количество тепла, проходящее через элементарный слой dr  с внутренним радиусом r:

Q = - lF ( );

F = 2prl;

Q = - dt/dR;

dR = dr/(2pllr) – тепловое сопротивление элементарного слоя.

Общее тепловое сопротивление определяется по формуле:

R = 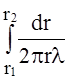 = (1/(2pll))ln(r₂/r₁) = (1/(2pll))ln(d₂/d₁),

d₁, d₂ – соответственно, внутренний и внешний диаметры  трубы, м.

Окончательно имеем:

Q = (t₁ – t₂)/R,   Вт;                                       (3.7)

t₁, t₂ – температуры, соответственно, внутренней и внешией поверхностей цилиндрической стенки. °С; t₁ > t₂.