













11 Кратные, криволинейные, поверхностные интегралы
11.1 Мера Жордана
Мы приступаем к интегрированию функций нескольких переменных. В определениях и свойствах новых типов интегралов многое будет похожим на случай одномерного интеграла Римана, рассмотренный подробно в 7 модуле. Однако здесь нам потребуется уточнить понятия площади и объёма. Напомним: вычисляя в разделе 7.5 площади и объёмы, мы пользовались лишь интуитивными представлениями. Теперь перейдём к точным определениям.
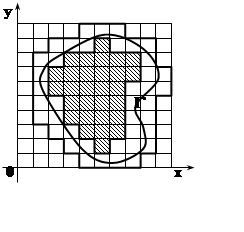
Рассмотрим на плоскости ограниченное множество Е. Разобъём плоскость на замкнутые (включающие границы) квадраты со стороной h с помощью вертикальных и горизонтальных прямых:
x= 0, x= ±h,x= ±2h, ...; y= 0, y= ±h, y= ±2h, ... .
 Пусть
Пусть 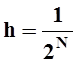 .
Обозначим
.
Обозначим ![]() – объединение тех квадратов,
которые целиком лежат внутри Е.
Пусть также
– объединение тех квадратов,
которые целиком лежат внутри Е.
Пусть также ![]() – объединение тех квадратов, которые
имеют с Е непустое пересечение.
Можно назвать
– объединение тех квадратов, которые
имеют с Е непустое пересечение.
Можно назвать ![]() и
и ![]() внутренней и внешней ступенчатыми
фигурами соответственно. Площадь одного квадрата равна h2 . Площади (или меры )
ступенчатых фигур обозначим m(
внутренней и внешней ступенчатыми
фигурами соответственно. Площадь одного квадрата равна h2 . Площади (или меры )
ступенчатых фигур обозначим m(![]() ),
m(
),
m(![]() ) –это
суммы площадей соответствующих квадратов.
) –это
суммы площадей соответствующих квадратов.
Заметим, что
при переходе от 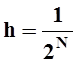 к
к 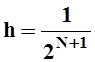 (т.е. при измельчении разбиения),
каждый квадрат делится на 4. При этой внутренняя ступенчатая фигура может
увеличиться, а внешняя – уменьшиться:
(т.е. при измельчении разбиения),
каждый квадрат делится на 4. При этой внутренняя ступенчатая фигура может
увеличиться, а внешняя – уменьшиться:
![]()
![]()
Переходя к площадям, получаем неравенства:
![]()
![]()
Рассмотрим числовую
последовательность ![]() . Она возрастает и
ограничена сверху (например, любым из чисел
. Она возрастает и
ограничена сверху (например, любым из чисел ![]() ). Значит, она имеет предел:
). Значит, она имеет предел:
![]() .
.
Назовём число ![]() внутренней мерой множества
Е. Аналогично, существует
внутренней мерой множества
Е. Аналогично, существует ![]() – внешняя мера Е. Множество Е называется измеримым по Жордану
, если внешняя мера совпадает с внутренней:
– внешняя мера Е. Множество Е называется измеримым по Жордану
, если внешняя мера совпадает с внутренней:
![]() .
.
Число m(E) в этом случае называется мерой Жордана множества Е. Впрочем, можно пользоваться и привычным словом «площадь».
Таким же образом, с помощью трёхмерной меры Жордана, уточняется понятие «объём». При необходимости перехода к более высоким размерностям, аналогично вводится понятие n– мерной меры Жордана, обобщающее понятия площади и объёма.
Перейдём к свойствам меры Жордана, подробно рассматривая плоский (n=2) случай.
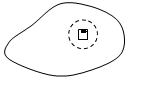 Ясно,
конечно, что отрицательной мера быть не может: если Е измеримо, то m(E)³0. Если E имеет
хотя бы одну внутреннюю точку, то m(E)>0.
Действительно, внутренняя точка входит в Е
вместе с некоторой окрестностью Ue.При достаточно мелких разбиениях в
окрестность Ue обязательно
попадёт хотя бы один из квадратов. Значит, внутренняя мера будет положительной.
Ясно,
конечно, что отрицательной мера быть не может: если Е измеримо, то m(E)³0. Если E имеет
хотя бы одну внутреннюю точку, то m(E)>0.
Действительно, внутренняя точка входит в Е
вместе с некоторой окрестностью Ue.При достаточно мелких разбиениях в
окрестность Ue обязательно
попадёт хотя бы один из квадратов. Значит, внутренняя мера будет положительной.
Множество, состоящее из одной точки, имеет, очевидно, меру 0. Множества меры 0 играют важную роль, как видно из следующей теоремы.
Теорема 1 (критерий измеримости). Пусть Е –ограниченное множество, Г – его граница (т.е. множество граничных точек). Тогда Е измеримо Û m(Г) = 0.
Доказательство.
Рассмотрим разбиение плоскости с шагом 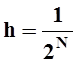 .
Пусть DN – множество,
состоящее из точек тех квадратов, которые входят в
.
Пусть DN – множество,
состоящее из точек тех квадратов, которые входят в ![]() ,
но не входят в
,
но не входят в ![]() . Это ступенчатое
замкнутое множество (так как квадраты включают границы), причём ("N)
. Это ступенчатое
замкнутое множество (так как квадраты включают границы), причём ("N)
![]() .
.
(Напомним: ![]() – объединение квадратов, пересекающихся с Г.) Отсюда следует, что
– объединение квадратов, пересекающихся с Г.) Отсюда следует, что
![]() .
(*)
.
(*)
Заметим также, что ![]() .
.
Допустим теперь, что Еизмеримо. Тогда
![]() .
.
Используя левое из неравенств (*), получаем,
что ![]() , а значит m(Г)= 0.
, а значит m(Г)= 0.
Обратно,
если m(Г) = 0 ,
то ![]() . Используя правое из неравенств (*), видим,
что lim m(DN)=0 , т.е.
. Используя правое из неравенств (*), видим,
что lim m(DN)=0 , т.е. ![]() , множество Е измеримо.
, множество Е измеримо.
Важность теоремы 1 объясняется тем, что множество точек гладкой (или кусочно–гладкой) кривой на плоскости имеет двумерную меру 0. Это вытекает из следующего результата.
Теорема 2. График Г непрерывной функции y = f(x), xÎ[a,b], имеет двумерную меру 0.
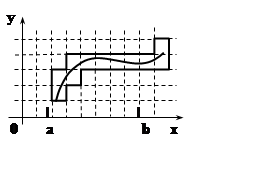 Доказательство.
По теореме Кантора, функция f(x) равномерно
непрерывна на [a, b], т.е. "e>0 $d>0:|x¢–x²|<dÞ|f(x¢)–f(x²)|<e.Уменьшая
d, можно
считать, что d< e. Рассмотрим разбиение плоскости с шагом
Доказательство.
По теореме Кантора, функция f(x) равномерно
непрерывна на [a, b], т.е. "e>0 $d>0:|x¢–x²|<dÞ|f(x¢)–f(x²)|<e.Уменьшая
d, можно
считать, что d< e. Рассмотрим разбиение плоскости с шагом ![]() . Подсчитаем площадь ступенчатой
фигуры
. Подсчитаем площадь ступенчатой
фигуры ![]() . Так как h< d, то из равномерной непрерывности следует, что высота
каждого «столбика» фигуры
. Так как h< d, то из равномерной непрерывности следует, что высота
каждого «столбика» фигуры ![]() не более e+2h. Площадь этого столбика не более (e+2h)h.
Количество столбиков не превышает
не более e+2h. Площадь этого столбика не более (e+2h)h.
Количество столбиков не превышает ![]() . (Просто
. (Просто ![]() взять нельзя потому, что это число
может оказаться меньшим, чем число столбиков.) Площадь фигуры
взять нельзя потому, что это число
может оказаться меньшим, чем число столбиков.) Площадь фигуры ![]() оценим сверху:
оценим сверху:
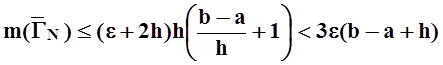 .
.
Теперь ясно, что, измельчая
разбиения, можно сделать площадь ![]() меньше любого
данного числа. Значит,
меньше любого
данного числа. Значит, ![]() . А тогда и m(Г)= 0.
. А тогда и m(Г)= 0.
Следствие. Множество на плоскости, ограниченное кусочно–гладкой кривой, измеримо.
 Доказательство.
Напомним: кривая, заданная уравнением F(x,y)= 0,
называется гладкой, если частные производные
Доказательство.
Напомним: кривая, заданная уравнением F(x,y)= 0,
называется гладкой, если частные производные ![]() ни
в одной её точке не равны 0
одновременно. Теорема о существовании неявной функции (теорема 5, 10.3) утверждает, что тогда в окрестности каждой точки кривая
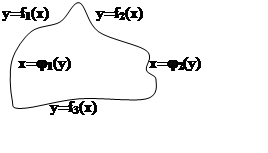
является либо графиком функции y= f(x), либо графиком функции x= j(y). Один из возможных случаев изображён
на рисунке. По теореме 2, мера каждого участка границы равна 0. Значит, мера всей границы равна 0. По теореме 1, множество измеримо.
ни
в одной её точке не равны 0
одновременно. Теорема о существовании неявной функции (теорема 5, 10.3) утверждает, что тогда в окрестности каждой точки кривая
является либо графиком функции y= f(x), либо графиком функции x= j(y). Один из возможных случаев изображён
на рисунке. По теореме 2, мера каждого участка границы равна 0. Значит, мера всей границы равна 0. По теореме 1, множество измеримо.
Следствие показывает, что подавляющее большинство ограниченных множеств, с которыми мы работаем, измеримы. Приведём пример неизмеримого по Жордану множества.
Пусть Т –множество точек в квадрате [0,1]´[0,1], имеющих рациональные координаты:
T={ (x,y) ç 0£x£1, 0£y£1; x,yÎQ }
Тогда, при любом разбиении, ![]() , т.е.
, т.е. ![]() .
С другой стороны, все квадраты разбиения будут содержать точки Т, поэтому
.
С другой стороны, все квадраты разбиения будут содержать точки Т, поэтому ![]() ,
т.е.
,
т.е. ![]() . Так как
. Так как ![]() ,
то Т –
неизмеримое множество.
,
то Т –
неизмеримое множество.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.