В заключение раздела докажем, что объединение, пересечение, разность измеримых множеств E1, E2 являются измеримыми множествами, причём если E1, E2 пересекаются лишь по граничным точкам (или не пересекаются), то
m(E1ÈE2) = m(E1) + m(E2).
Действительно, любая граничная точка множества E1ÈE2 является граничной либо для E1, либо для E2, т.е.
Г(E1ÈE2) Í Г(E1) ÈГ(E2).
По теореме 1, множества Г(E1),Г(E2)имеют меру 0. Поэтому Г(E1ÈE2) тоже множество меры 0. Значит, по теореме 1, E1ÈE2 измеримо.
Аналогично проверяется, что E1ÇE2, E1èE2 измеримы.
Пусть теперь в пересечении E1ÇE2 есть лишь граничные точки. Ясно, что
.
Так как для ступенчатых фигур очевидно:
, 
, то в общем случае получаем:
.
Переходим к пределу при N®¥ :
m(E1)+ m(E2)= m(E1ÈE2).
Все рассмотренные свойства меры справедливы и в пространствах более высоких размерностей. В частности, множество в R3, ограниченное кусочно–гладкими поверхностями, измеримо (т.е. имеет объём).
11.2 Двойные и тройные интегралы
11.2.1 Определение и свойства кратных интегралов.Пусть Е – ограниченное измеримое множество на плоскости. Функция f(x,y) определена на Е. Рассмотрим разбиение Е с помощью кусочно–гладких кривых:
E= E1ÈE2È...ÈEn.
Тогда все Еi измеримы, причём m(E)= m(E1)+...+m(En).
В каждом множестве Еi
выберем произвольно точку Pi.
Составим сумму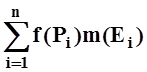 
, она называется интегральной
суммой Римана.
Введём понятие мелкости разбиения. Диаметром множества AÍR2 называется число
т.е. диаметр – точная верхняя грань расстояний между точками множества. Мелкостью разбиения Е= E1È...ÈEn называется число
d= max {d(Ei)}.
Двойным интегралом от функции f(x, y) по множеству Е называется такое число I, что
"e>0 $d>0: для любого разбиения мелкостью меньше d, при любом выборе точек PiÎEi
.
Только в смысле этого точного определения допустима символическая запись
.
В точности так же для функции f(x, y, z), определённой на измеримом множестве EÍR3 , вводится понятие тройного интеграла. Аналогично можно ввести и рассматривать интегралы более высоких размерностей, но это не входит в нашу программу.
Для двойного и тройного интегралов наиболее употребительны обозначения:
Рассмотрим общие свойства кратных (т.е. двойных, тройных, и т.д.) интегралов. Работать, в основном, будем с двойными интегралами, имея ввиду, что для тройных и формулировки, и доказательства сохраняются.
Многие из свойств аналогичны и случаю одномерного интеграла Римана – в 7 модуле они подробно доказаны. Здесь же мы иногда опускаем подробности доказательств.
Свойство
1. Если C= const, то 
. В
частности,
–
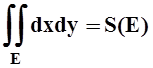площадь плоской фигуры Е,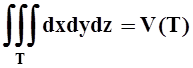 
– объём тела Т.
Доказательство очевидно: если f(x,y)= C, то все интегральные суммы равны между собой:
Свойство 2. Если m(E) = 0, то для любой функции
.
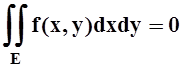Доказательство. Если Е = E1ÈE2È...ÈEn, m(E) = 0, то m(Ei)=0 ("i). Поэтому любая интегральная сумма равна 0.
Свойство 3 (линейность). Если a, bÎR, то
.
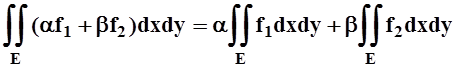Cвойство 4. Если "PÎE f1(P) £ f2(P), то
.
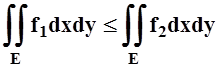Доказательство свойств 3, 4 следуют из соответствующих свойств интегральных сумм и определения интеграла.
Свойство 5 (аддитивность). Если Е = E1ÈE2, причём разбиение проведено кусочно–гладкой кривой, и соответствующие интегралы существуют, то
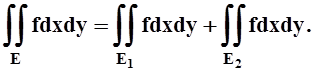
Доказательство.Разбиения множеств E1, E2 образуют разбиение множества E. Сумма
является интегральной суммой для функции f на множестве E. При измельчении разбиений, в пределе получаем требуемое соотношение.
Свойство 6 (оценка модуля интеграла).
.
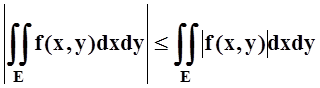Доказательство. К очевидному неравенству
– | f(x,y)|£ f(x,y) £| f(x,y) |
применим свойство 4. Получим:
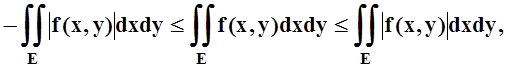
что равносильно требуемому неравенству.
Свойство
7 (теорема о среднем). Пусть функция f(x,
y) непрерывна на компактном
связном множестве Е. Тогда 
.
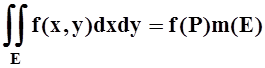Доказательство.Если m(E) = 0, то интеграл равен 0, и равенство справедливо для любой точки P. Пусть m(E) ¹ 0. Непрерывная на компактном множестве функция ограничена и достигает своих точных граней. Пусть
, f(P1)£f(x,y)£ f(P2).
Применяя свойства 4 и 1, отсюда получаем:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.