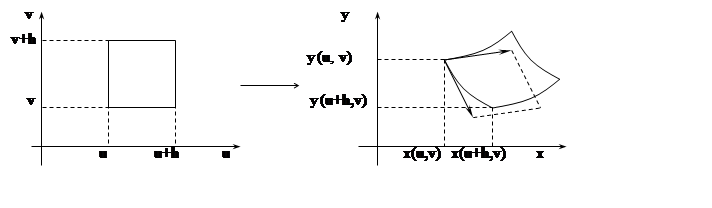 |
Пренебрегая бесконечно малыми величинами более высоких (по сравнению с h) порядков, заменим «секущий» вектор
(x(u+h, v)–x(u, v), y(u+h, v)–y(u,v))
на касательный вектор 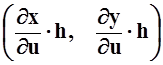 . Аналогично, «секущий»
вектор (x(u,v+h)–x(u,v), y(u,v+h)–y(u,v)) заменим на касательный вектор
. Аналогично, «секущий»
вектор (x(u,v+h)–x(u,v), y(u,v+h)–y(u,v)) заменим на касательный вектор 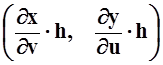 .
.
Найдём площадь параллелограмма, построенного на касательных векторах:
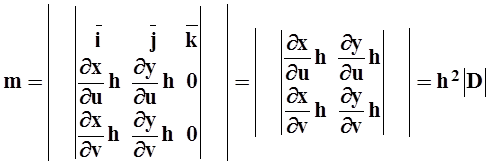 .
.
(Сначала вычисляется векторное произведение, затем его модуль, равный площади параллелограмма). Можно доказать, что площадь «криволинейного параллелограмма» отличается от вычисленной на бесконечно малую более высокого порядка, чем h2, т.е. равна
h2|D| + e(h)×h2 = (|D|
+ e(h))h2, где ![]() .
.
Рассмотрим интегральную сумму для нашего разбиения области Е (включая в неё лишь те параллелограммы, которые целиком принадлежат области):
![]()
![]()
Первое слагаемое здесь –
интегральная сумма для интеграла 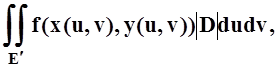 соответствующая
рассматриваемому разбиению Е¢ на квадраты. Второе
слагаемое стремится к 0 при
неограниченном измельчении разбиения. Действительно, функция f непрерывна на компактном множестве, а
следовательно ограничена:
соответствующая
рассматриваемому разбиению Е¢ на квадраты. Второе
слагаемое стремится к 0 при
неограниченном измельчении разбиения. Действительно, функция f непрерывна на компактном множестве, а
следовательно ограничена: ![]() . Поэтому
. Поэтому
![]()
при h®0. Переходя к пределу при h®0, получим требуемую в теореме формулу.
Наиболее часто мы будем использовать замену переменных, связанную с переходом от декартовой системы координат к полярным координатам. Напомним: декартова и полярная система координат называются согласованными, если полюс совпадает с началом декартовой системы, а полярная ось – с осью OX. В этом случае декартовы x, y и полярные r, jкоординаты одной и той же точки связаны формулами:
x= rcosj,y= rsinj.
Вычислим якобиан такой замены переменных:
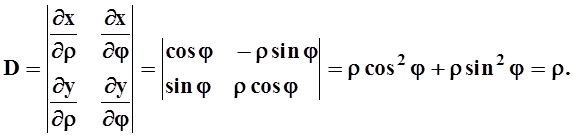
Формула, рассмотренная в теореме 7, принимает вид:
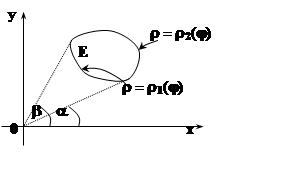
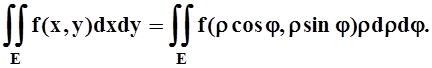
(Здесь можно не вводить новое обозначение для области интегрирования – область Е остаётся неизменной, лишь её точки приобретают новые координаты). Как правило, сначала выполняется интегрирование по r(в пределах, зависящих в общем случае от j), а затем интегрирование по углу j– в пределах его наибольшего изменения:
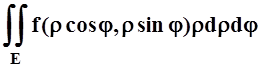
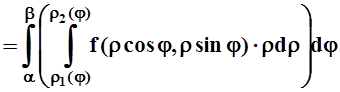 .
.
 Пример
3. Вычислить
Пример
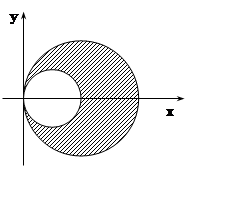
3. Вычислить 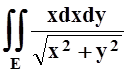 , если область Е ограничена окружностями x2+y2 = 2x, x2+y2 = 4x.
, если область Е ограничена окружностями x2+y2 = 2x, x2+y2 = 4x.
Решение. Выделяя полные квадраты, уравнения окружностей можно записать так:
(x–1)2+y2 = 1, (x–2)2+y2 = 4.
Теперь легко изобразить окружности, представить требуемую область Е. Однако для того, чтобы вычислить интеграл в полярной системе координат, нам нужно эти уравнения тоже записать в полярных координатах. Подставляя x= rcosj,y= rsinj,получим уравнения
r= 2 cosj,r= 4 cosj.
Угол j, очевидно, может принимать значения от
![]() до
до ![]() .
Переходим в полярную систему и вычисляем интеграл:
.
Переходим в полярную систему и вычисляем интеграл:
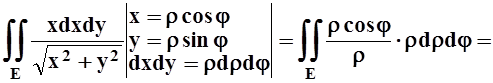
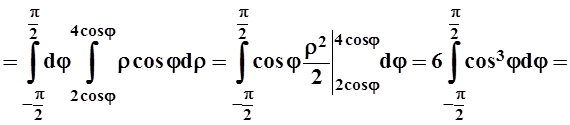
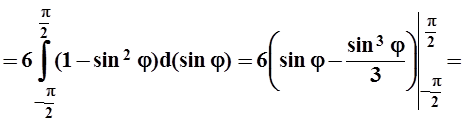
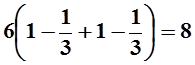 .
.
В тройных интегралах замена переменных проводится по аналогичной формуле:
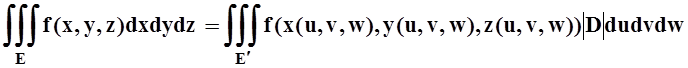 .
.
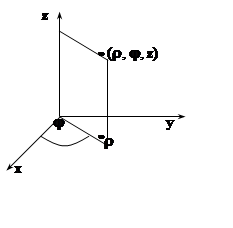 Наиболее
часто приходится использовать переход в цилиндрическую или сферическую системы
координат. Цилиндрические координаты точки – это полярные
координаты r и j её
проекции на плоскость XOY, а
также аппликата z.
Таким образом, переход в цилиндрическую систему координат проводится по
формулам:
Наиболее
часто приходится использовать переход в цилиндрическую или сферическую системы
координат. Цилиндрические координаты точки – это полярные
координаты r и j её
проекции на плоскость XOY, а
также аппликата z.
Таким образом, переход в цилиндрическую систему координат проводится по
формулам:
x= rcosj,y= rsinj,z= z.
Легко подсчитать, что якобиан такого преобразования равен r. В большинстве случаев использование цилиндрических координат равносильно интегрированию по переменной z, а затем переходу в полярную систему координат в полученном двойном интеграле.
 Пример
4. Вычислить
Пример
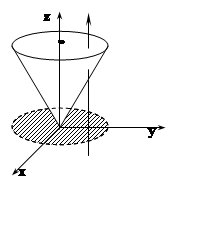
4. Вычислить 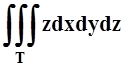 , если тело Т ограничено конической поверхностью x2+y2 = z2 и плоскостью z= 1.
, если тело Т ограничено конической поверхностью x2+y2 = z2 и плоскостью z= 1.
Решение.
Сделаем рисунок. Можно интегрировать по z (zизменяется от конуса, на котором ![]() , до плоскости z= 1), а затем, в
двойном интеграле по кругу, перейти к полярным координатам. Или, что то же
самое, перейти в цилиндрическую систему:
, до плоскости z= 1), а затем, в
двойном интеграле по кругу, перейти к полярным координатам. Или, что то же
самое, перейти в цилиндрическую систему:
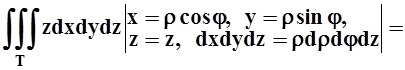
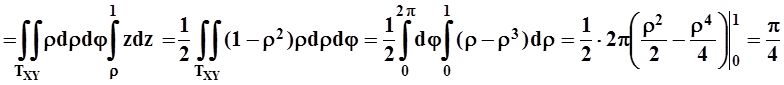 .
.
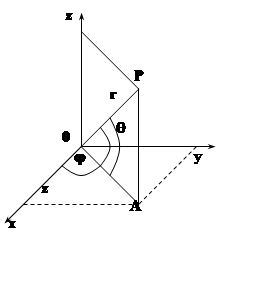 Важную роль играет сферическая
система координат. В этой системе положение точки Р задаётся числами r,j,q, причём
r= |OP| – расстояние от точки до начала
координат (r ³ 0), j–полярный
угол проекции А точки Р на плоскость
XOY (0 £ j< 2p), q–
угол между вектором
Важную роль играет сферическая
система координат. В этой системе положение точки Р задаётся числами r,j,q, причём
r= |OP| – расстояние от точки до начала
координат (r ³ 0), j–полярный
угол проекции А точки Р на плоскость
XOY (0 £ j< 2p), q–
угол между вектором ![]() и плоскостью XOY
и плоскостью XOY 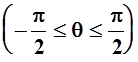 .
Рассматривая соответствующие треугольники, легко видеть, что
.
Рассматривая соответствующие треугольники, легко видеть, что ![]() ,
а
,
а
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.