Кратные, криволинейные, поверхностные интегралы. Мера Жордана, страница 3

.

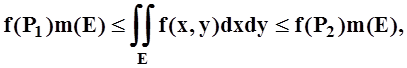
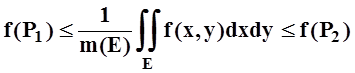Так как Е – связное множество, то, по теореме о промежуточных значениях, 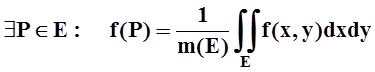,       что и требовалось доказать.

Дадим без доказательства очень важное достаточное условие интегрируемости функции.

Теорема 3. Если функция f непрерывна на измеримом компактном множестве Е, то она интегрируема на  Е.

Как и в случае одномерного интеграла, доказательство проводится с помощью сумм Дарбу. Можно усилить теорему 3: даже если функция разрывна в отдельных точках или на некоторых кучно–гладких кривых, она всё–таки будет интегрируемой. Для интегрируемости достаточно, чтобы множество точек разрыва имело меру 0. Кроме того, изменение значений функции в точках, множество которых имеет меру 0, не влияет ни на интегрируемость функции, ни на величину интеграла (если только функция остаётся ограниченной). В частности, если Е ограничено кусочно–гладкой кривой, то интеграл не зависит от значений в граничных точках.

Отметим, что мы рассматриваем интегралы только по измеримым множествам, которые с самого начала берутся ограниченными. Кроме того, если множество Е ограничено кусочно–гладкой кривой, то любая интегрируемая на Е функция ограничена. Интегралы от неограниченных функций, интегралы по неограниченным множествам мы не рассматриваем. Хотя есть подходы к определению и работе с такими (несобственными) интегралами.

11.2.2  Вычисление двойных и тройных интегралов в декартовых координатах.

Рассмотрим, на плоскости прямоугольную область :

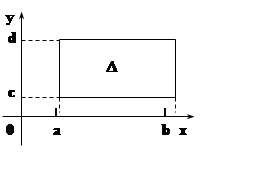D= [a, b]´[c, d] = { (x, y) ça£x£b, c£y£d}. Пусть на D определена функция  f(x, y).  Рассмотрим, функцию 

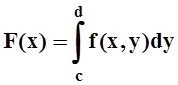, заданную в виде интеграла, зависящего от параметра.

Теорема 4.  Если  f(x, y)  непрерывна на D, то F(x) непрерывна на  [a, b].

Доказательство.  Возьмём  x₀Î[a, b].    Дадим  приращение  Dx  так, чтобы  x₀+Dx Î[a, b].  Вычислим приращение  DF:

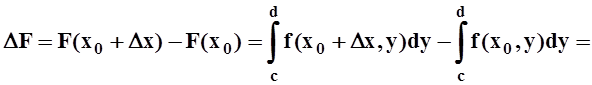
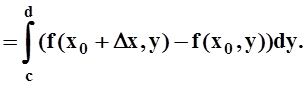
По теореме Кантора,  f(x, y)  равномерно непрерывна на  D:

"e> 0   $d> 0:  "P¢, P²ÎD   çP¢–P²ç < dÞ| f(P¢)–f(P²)| < e.

В нашем случае, конкретнее:

 .

(Как обычно, оценка с помощью    имеет тот же смысл, что и с помощью  e). Поэтому

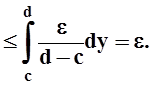
Итак,  "e> 0  $d> 0:   | Dx| < dÞ|DF| < e,  т.е.  ,  что и означает непрерывность функции  F(x)

Так как непрерывная функция интегрируема, то существует

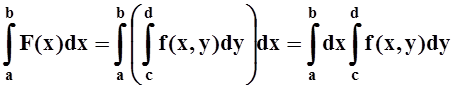
–  так называемый повторный интеграл. Последняя его запись экономит 2 скобки и является общепринятой, хотя, возможно, на первых порах удобнее пользоваться записью со скобками. Можно рассматривать и другой повторный интеграл, соответствующий другому порядку интегрирования:

.

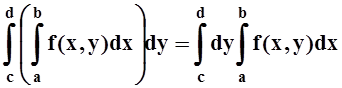Научимся вычислять двойной интеграл по прямоугольной области с помощью повторных интегралов.

Теорема 5.  Если  f(x,y)  непрерывна на  D, то

 .

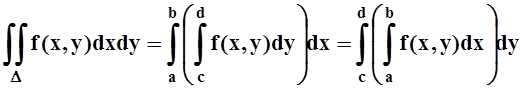Доказательство.  Все написанные интегралы существуют, так как интегрируются непрерывные функции.

Рассмотрим разбиения отрезков  [a,b]  и   [c,d]:

a= x₀,  x₁, x₂, ..., x_n = b;      c= y₀, y₁, y₂, ..., y_n = d.

Обозначим  D_ij = {(x, y) çx_i–1 £ x£x_i,  y_j–1 £ y£y_j }.  Тогда получаем разбиение Dна меньшие прямоугольники

.

Возьмём один из повторных интегралов и проведём преобразования (а затем поясним каждое действие).

=

.

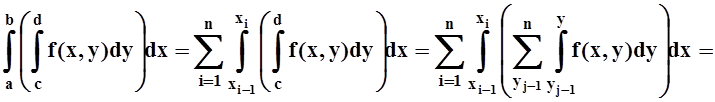
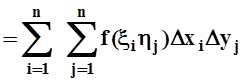Пояснения: 1) заменили интеграл по  [a,b]  на сумму интегралов по  [x_i–1,x_i],  т.е. использовали аддитивность;  2) то же самое для интеграла по  [c,d];  3) воспользовались линейностью: интеграл от суммы равен сумме интегралов; 4) по теореме о среднем, каждый из интегралов по  [x_i–1,x_i]  заменили на значение подинтегральной функции в некоторой точке  x_i,  умноженное на длину промежутка интегрирования  Dx_i = x_i–x_i–1;  5) аналогичное  действие с каждым из интегралов по  [y_j–1, y_j].

В результате получилась интегральная сумма для двойного интеграла 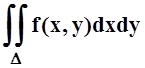,  правда, для разбиения специального вида (на прямоугольники). Но интеграл существует, поэтому при измельчении разбиений  интегральные суммы любого вида стремятся к интегралу. Переходя к пределу и учитывая, что в левой части равенства повторный интеграл не зависит от разбиений (это просто число), получим:

что и требовалось доказать.